Product Inequation
Solving a product inequality consists in finding the values of x that satisfy the condition established by the inequality. For this we use the study of the sign of a function. Note the resolution of the following product equation: (2x + 6)*( – 3x + 12) > 0.
Let's establish the following functions: y1 = 2x + 6 and y2 = – 3x + 12.
Determining the root of the function (y = 0) and the position of the line (a > 0 increasing and a < 0 decreasing).
y1 = 2x + 6
2x + 6 = 0
2x = – 6
x = –3 
y2 = – 3x + 12
–3x + 12 = 0
–3x = –12
x = 4 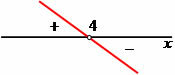
Checking the sign of the product inequality (2x + 6)*(– 3x + 12) > 0. Note that the product inequality requires the following condition: the possible values must be greater than zero, that is, positive.
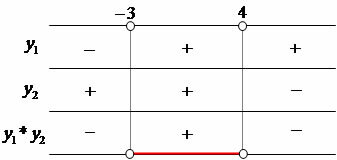
Through the scheme that demonstrates the signs of the product inequality y1*y2, we can reach the following conclusion regarding the values of x:
x Є R / –3 < x < 4
Do not stop now... There's more after the advertising ;)
quotient inequality
In solving the quotient inequality we use the same resources as the product inequality, what differs is that, by we calculate the denominator function, we need to adopt values greater than or less than zero and never equal to zero. Note the resolution of the following quotient inequality:
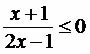
Solve the y functions1 = x + 1 and y2 = 2x – 1, determining the root of the function (y = 0) and the position of the line (a > 0 increasing and a < 0 decreasing).
y1 = x + 1
x + 1 = 0
x = -1
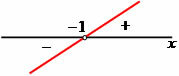
y2 = 2x - 1
2x - 1 = 0
2x = 1
x = 1/2
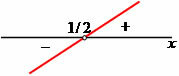

Based on the sign set, we conclude that x assumes the following values in the quotient inequality:
x Є R / –1 ≤ x < 1/2
by Mark Noah
Graduated in Mathematics
Brazil School Team
1st Degree Function - Roles - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Product Inequation and Quotient Inequation"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/inequacao-produto-e-quociente.htm. Accessed on June 28, 2021.