THE exponential function occurs when, in its formation law, the variable is in the exponent, with domain and counter-domain in the real numbers. The domain of the exponential function is the real numbers, and the counter domain is the nonzero positive real numbers. Your training law can be described by f(x) =Thex, on what The is a positive real number other than 1.
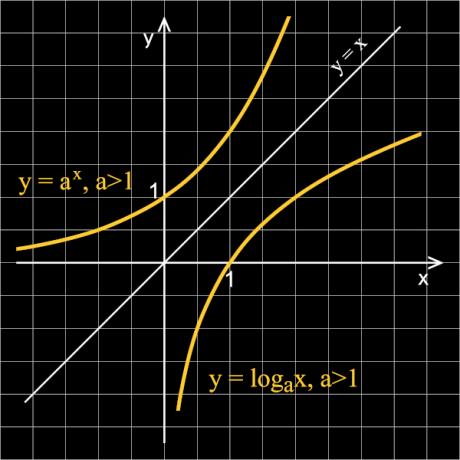
O graphic of an exponential function will always be in the first and second quadrants of the Cartesian plane, and may be increasing, when The is a number greater than 1, or decreasing when The is a positive number less than 1. THE inverse function of the exponential function is the logarithmic function, which makes the graphs of these functions always symmetrical.
Read too: What is function?
What is an exponential function?
As the name suggests, the term exponential is linked to exponent. So the exponential function definition is a function whose domain is the set of real numbers, and the counterdomain is the set of non-zero positive real numbers.
, described by : ℝ → ℝ*+. Its formation law is described by the equation f (x) = Thex, on what The is any real number, positive, not null and given the base name.Examples:

In the formation law, f (x) can also be described as y and, as in the other functions, it is known as a dependent variable, because its value depends on x, which is known as a variable. independent.
Do not stop now... There's more after the advertising ;)
Exponential Function Types
The exponential functions can be classified into two distinct cases. Taking into account the behavior of the function, it can be ascending or descending.
An exponential function is called increasing if, as the value of x increases, the value of f(x) also increases. This occurs when the base is greater than 1, that is: The > 1.
Example:

An exponential function is considered decreasing if, as the value of x increases, the value of f(x) decreases. This occurs when the base is a number between 0 and 1, that is, 0 < The < 1.
Example:

Read too: Differences between function and equation
Exponential Function Graph
In order to draw the graphical representation of an exponential function, it is necessary to find the image for some domain values. The graph of an exponential function has the characteristic of a growth much greater than that of linear functions, if increasing, or a greater decrease, when decreasing.
Examples:
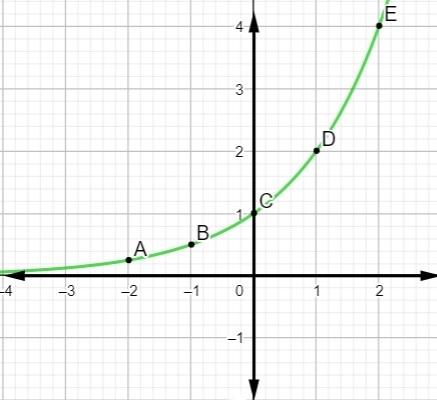
a) Build the graph of the function: f (x) = 2x.
Since >1, then this function is increasing. To build the graph, let's assign some values to x as shown in the table below:

Now that we know some points of the function, it is possible to mark them in the Cartesian plane and plot the exponential function curve.
b) Build the graph of the following function:
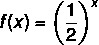
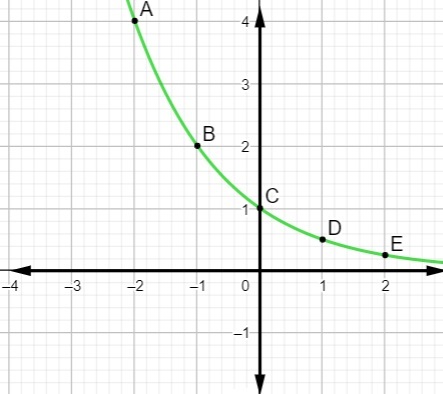
In this case, the function is descending, since the base is a number between 0 and 1, then the graph will be descending.

After finding some numerical values, it is possible to represent the graph of the function in the Cartesian plane:
Exponential Function Properties
→ 1st property
In any exponential function, regardless of its base value The, We have tof (0) = 1. After all, we know this is a potency property, that is, every number raised to 0 is 1. This means that the graph will intersect the vertical axis at point (0.1) every time.
→ 2nd property
The exponential function is injector. Data x1 and x2 such that x1 ≠ x2, so the images will also be different, ie f(x1) ≠ f(x2), which means that for each image value, there is a single value in the domain that corresponds to that image.
Being injective means that for values other than y, there will be a single value of x that makes f(x) equal to y.
→ 3rd property
It is possible to know the behavior of the function according to its base value. The graph will grow if the base is greater than 1 (The > 1) and decreasing if the base is less than 1 and less than 0 (0 < to < 1).
→ 4th property
O graph of the exponential function is always in the 1st and 2nd quadrants, because the counterdomain of the function are the nonzero positive reals.
Read too: How to graph a function?
Exponential function and logarithmic function
As the exponential function is a function that admits inverse, this comparison between exponential function and logarithmic function is inevitable. turns out that the logarithmic function is the inverse function of the exponential. The graphs of these functions are symmetric about the x-axis bisector. Being an inverse function means that the logarithmic function does the opposite of what the exponential function does, that is, in the exponential function, if f (x) = y, then the logarithmic function, being inverse, will be denoted by f-1 the f-1 (y) = x.
solved exercises
(Enem 2015) The workers union of a company suggests that the salary floor of the class is R$ 1,800.00, proposing a fixed percentage increase for each year dedicated to work. The expression that corresponds to the salary proposal (s), as a function of length of service (t), in years, is s (t) = 1800·(1,03)t.
According to the union's proposal, the salary of a professional from this company with 2 years of service will be, in reais,
a) 7,416.00
b) 3,819.24
c) 3,709.62
d) 3,708.00
e) 1909.62
Resolution:
We want to calculate the image of the function when t = 2, that is, s(2). Substituting t = 2 in the formula, we will find that:
s (2) = 1800 · (1.03)²
s(2) = 1800 · 1.0609
s(2) = 1909.62
Alternative E
2) (Enem 2015) The addition of technologies in the industrial production system aims to reduce costs and increase productivity. In the first year of operation, an industry manufactured 8000 units of a particular product. The following year, it invested in technology, acquiring new machines and increased production by 50%. It is estimated that this percentage increase will be repeated in the coming years, guaranteeing an annual growth of 50%. Let P be the annual quantity of products manufactured in the year t of the industry's operation.
If the estimate is reached, what is the expression that determines the number of units produced Pin function of t, for t ≥ 1?
The) P(t) = 0.5 · t -1 + 8 000
B)P(t) = 50 · t -1 + 8000
ç)P(t) = 4 000 · t-1 + 8 000
d)P(t) = 8 000 · (0,5)t-1
and)P(t) = 8 000 · (1,5)t-1
Resolution:
Note that there is a relationship between the year t and the quantity of a certain product P. Knowing that there is an increase of 50% for each year, this means that, when comparing the production of a year before and after, the value of the second corresponds to 150%, which is represented by 1.5. Knowing that the initial production is 8000 and that, in the first year, this was the production, we can describe this situation by:
In the first year, that is, if t= 1 → s (t) = 8 000.
In the second year, if t = 2 → P(2) = 8 000 · 1,5.
In the third year, if t = 3 → P(3) = 8 000 · 1,5 · 1,5 = 8 000 · 1,5².
After t years, we will have P(t) = 8 000 · (1,5)t-1.
Alternative E
By Raul Rodrigues de Oliveira
Maths teacher


