Step-by-step construction of the graph of the second degree function

In Elementary School, functions are mathematical formulas that associate each number in a numerical set (the domain) with a single number belonging to another set (the counterdomain). When this formula is a second degree equation, we have one high school function.

Functions can be represented by geometric figures whose definitions coincide with their mathematical formulas. This is the case of the straight line, which represents functions of the first degree, and the parable, which represents functions of the second degree. These geometric figures are called graphics.

The central idea of ​​function representation by a graph

For graph a function, it is necessary to evaluate which element of the counterdomain is related to each element of the domain and mark them, one by one, in a Cartesian plane. When all these points are scored, the result will be just the graph of a function.

It is noteworthy that the high school functions, are usually defined in a domain equal to the entire set of real numbers. This set is infinite and, therefore, it is impossible to mark all its points on a Cartesian plane. Thus, the alternative is to sketch a graph that can partially represent the evaluated function.

First of all, remember that second-degree functions take the following form:

y = ax² + bx + c

Therefore, we present five steps that make it possible to build a second degree function graph, exactly like those required in High School.

Step 1 – Overall job evaluation

There are some indicators that help you find out if the right path is being taken when building the high school function graph.

I - The coefficient "a" of a high school function indicates its concavity, that is, if a > 0, the parabola will be upwards and will have a minimum point. If a < 0, the parabola will be down and have a maximum point.

II) The first point A of the graph of a parable it can be easily obtained just by looking at the value of the coefficient “c”. Thus, A = (0, c). This happens when x = 0. Watch:

y = ax² + bx + c

y = a·0² + b·0 + c

y = c

Step 2 – Find the vertex coordinates

the apex of a parable is its maximum (if a < 0) or minimum (if a > 0) point. It can be found by substituting the values ​​of coefficients “a”, “b” and “c” in the formulas:

x_v = - B
2nd

y_v = –∆
4th

Thus, vertex V is given by the numerical values ​​of x_v and y_v and it can be written like this: V = (x_vyy_v).

Step 3 – Random points on the graph

It is always good to indicate some random points whose values ​​assigned to the variable x are greater and less than x_v. This will give you points before and after the vertex and will make drawing the graph easier.

Step 4 – If possible, determine the roots

When they exist, the roots can (and should) be included in the design of the graph of a function of the second degree. To find them, set y = 0 to get a quadratic equation that can be solved by Bhaskara's formula. remember that solve a quadratic equation is the same as finding its roots.

Do not stop now... There's more after the advertising ;)

THE Bhaskara formula it depends on the formula of the discriminant. Are they:

x = – b ± √∆
2nd

∆ = b² – 4ac

Step 5 – Mark all the points obtained on the Cartesian plane and link them together, in order to build a parabola

Remember that the Cartesian plane is made up of two perpendicular number lines. This means that, in addition to containing all the real numbers, these lines form a 90° angle.

Example of Cartesian plan and example of a parable.

Example

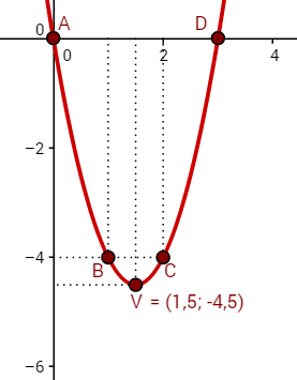
Plot the second degree function y = 2x² – 6x.

Solution: Note that the coefficients of this parabola are a = 2, b = – 6 and c = 0. In this way, by the step 1, we can say that:

1 – The parabola will be up, as 2 = a > 0.

2 – One of the points of this parable, represented by the letter A, is given by the coefficient c. Soon, A = (0.0).

by step 2, we observe that the vertex of this parabola is:

x_v = - B
2nd

x_v = – (– 6)
2·2

x_v = 6
4

x_v = 1,5

y_v = – ∆
4th

y_v = – (B² – 4·a·c)
4th

y_v = – ((– 6)² – 4·2·0)
4·2

y_v = – (36)
8

y_v = – 36
8

y_v = – 4,5

Therefore, the vertex coordinates are: V = (1.5, – 4.5)

Using the step 3, we will choose only two values ​​for the variable x, one greater and one less than x_v.

If x = 1,

y = 2x² – 6x

y = 2·1² – 6·1

y = 2·1 - 6

y = 2 - 6

y = – 4

If x = 2,

y = 2x² – 6x

y = 2·2² – 6·2

y = 2·4 – 12

y = 8 - 12

y = – 4

Therefore, the two points obtained are B = (1, – 4) and C = (2, – 4)

Fur step 4, which does not need to be done if the function has no roots, we get the following results:

∆ = b² – 4ac

∆ = (– 6)² – 4·2·0

∆ = (– 6)²

∆ = 36

x = – b ± √∆
2nd

x = – (– 6) ± √36
2·2

x = 6 ± 6
4

x' = 12
4

x' = 3

x'' = 6 – 6
4

x'' = 0

Therefore, the points obtained through the roots, considering that, to obtain x = 0 and x = 3, it was necessary to set y = 0, are: A = (0, 0) and D = (3, 0).

With that, we get six points to draw the graph of the function y = 2x² – 6x. Now just fulfill the step 5 to definitely build it.

By Luiz Paulo Moreira
Graduated in Mathematics