Periodic functions are those in which the function values (f (x) = y) repeat for certain values. of the variable x, that is, for each period determined by the values of x, we will obtain repeated values for the occupation.
Let's look at an example to better understand this definition:
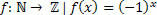
Let's make a table with some values for the variable x, listing the value of the function for each value of x.
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| f(x) | 1 | -1 | 1 | -1 | 1 | -1 |
Note that f (x)= 1 occurs only when the value of the variable x it's pair.
Note that f (x)= –1 occurs only when the value of the variable x is odd.
Do not stop now... There's more after the advertising ;)
That is, this is a periodic function, in which we have two different periods, one in which the value of the function is 1 (f (x)= 1) and the other in which the function is –1 (f (x)= –1 ).
Note also that when x varies by two units, the value of the function is repeated, that is: f (x) = f (x+2) = f (x+4) = f (x+6)... Thus, we can say that the period of this function is 2.
Therefore, we can define periodic functions as follows:
“A function is called periodic if there is a real number p > 0, such that: f (x)=f (x+p). Thus, the smallest value of p, which satisfies this equality, is called time course of the f” function.
Thus, if: f (x) = f (x+1.5) = f (x+3) = f (x+4.5), it is a periodic function whose period p = 1.5 .
In trigonometric functions, we have examples of periodic functions such as sine function, cosine function, tangent function.
Example:
y = cos x
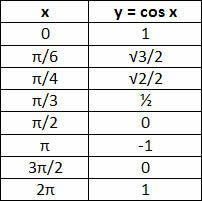
See that the value 1 repeats in a period p = 2π, and that the value y = 0 repeats in a period p = π.
By Gabriel Alessandro de Oliveira
Graduated in Mathematics
Brazil School Team
Would you like to reference this text in a school or academic work? Look:
OLIVEIRA, Gabriel Alessandro de. "Periodic functions"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/funcoes-periodicas.htm. Accessed on June 27, 2021.