THE financial math is one of the areas of mathematics responsible for studying phenomena related to the financial world. In addition, studying their concepts is very important, since, in our daily lives, they are increasingly more gifts, for example, when we receive a discount when buying something in cash or an extra when buying something installments.
Studying financial math requires prior knowledge of percentage, we will see that all concepts are based on this theme.
Read too:Percentage calculation with rule of three
What is financial math for?
Financial math is used daily, for example, when we are going to make a cash purchase and the seller offers a discount 5% on the value of the product, or when we choose to purchase a product in installments and, in this process, a interest rate it is billed to the buyer over time.
An example of the importance of understanding the concepts of financial mathematics is called overdraft limit. When opening an account at a certain bank, “extra” money is offered, for emergencies, for example. However, when using this limit or part of it, a fee to be paid later is charged, in addition to the money taken. This rate is called interest, and by better understanding these concepts, we can devise a better strategy for managing our finances.
Example 1
A person needs 100 reais to finish paying their monthly bills, however their entire salary has already been spent on the other bills. In analysis, this person found that he had two options.
Option 1 – Use the overdraft limit offered by the bank, at a rate of 0.2% per day, to be paid in one month.
Option 2 – Get the 100 reais from a friend, at a rate of 2% per month, to be paid for two months.
Using only the knowledge of percentage, let's analyze which is the best option.
analyzing the option 1, note that the rate of 0.2% is charged per day, that is, 0.2% of the loan amount is added each day, like this:

How the loan must be paid in a month, and considering the month with 30 days, the amount of interest to be paid is:
0,2 ·30
6
Thus, we can conclude that the amount to be paid at the end of a month is:
100 + 6= 106 reais
100 → Amount lent by the bank
6 → Interest amount
Now analyzing the option 2, the fee charged is 2% per month and must be paid within two months, that is, every month, 2% of the borrowed amount is added to the debt, like this:

Note that 2 reais per month must be added to the debt amount:
2 · 2 = 4
Therefore, the amount to be paid at the end of the period is:
100+ 4 = 104 reais
100 → Amount borrowed by the friend
4 → Interest amount
So, we can conclude that the best option is to take the money with the friend. This is a simple and important application of financial mathematicsOf course there are more sophisticated problems, tools and concepts, but like everything else in life, before understanding the complex part, it is necessary to understand the basics.
Do not stop now... There's more after the advertising ;)
Basics of Financial Mathematics
The main concepts of financial mathematics involve prior knowledge about percentages. Next, we will see concepts such as addition, discount, simple interest and compound interest.
addition
The idea of the addition is associated with add or add part of the value to its original value, that is, we add a percentage of a certain value to itself. See the example:
Example 2
A product cost 35 reais, with the increase in the dollar, it increased by 30%. Determine the new value for this product.
Oftentimes, when we go to do the addition-related calculations, they are performed wrongly by writing:
35 + 30%
The percentage represents part of something, so for this account to be correct, we must first calculate 30% of the initial value, in this case 35. Thus:
35 + 30% of 35
Solving the percentage first and then adding the values together, we will have to:
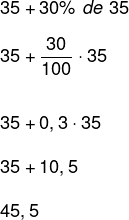
Therefore, with the addition, the value in the product will be 45.5 reais (forty-five reais and fifty cents).
Generally speaking, we can deduce a formula for addition. Consider an x value and that it increases by p%. According to what we have just defined, we can write this addition as follows:
x + p% of x
Developing this expression, we will have to:

Let's redo example 2 using the formula above. Note that x = 35 and the increase was 30%, that is, p = 30%.
35 · (1 + 0,01 · 30)
35 · (1 + 0,3)
35 · 1,3
45,5
Note that the same value was obtained, and it is an option to use such a formula.
See too: Inversely proportional quantities
Discount
The idea of discounting is similar to the idea of adding, the only difference is that instead of adding, we should subtract a percentage of the original value.
Example 3 – A product that costs 60 reais, when purchased in cash, has a 30% discount. Determine the new value for this product.
Similar to the addition, we will have to:
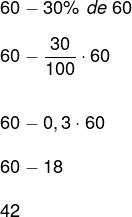
Analogously to the addition, we can deduce a discount formula. Consider a value x and that it suffers a discount of p%. According to what we defined, we can write this addition as follows:
x - p% of x
Developing this expression, we will have to:
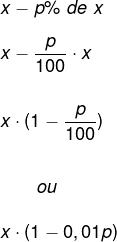
Let's redo example 3 using the formula above, note that x = 60 and the increase was 30%, that is, p = 30%.
x · (1 - 0.01p)
60 · (1 – 0,01 · 30)
60 · (1 – 0,3)
60 · 0,7
42
See that, using the formula, we got the same result, so in the discount we also have two options to determine it.
simple interest
The idea behind the simple interest it's also similar to the idea of addition, the difference between them is given by the period in which they are calculated. While the surcharge rate is applied once, the simple interest rate is calculated in a time interval. We can calculate the simple interest of a given capital C, applied at a given rate at a simple interest regime (i), in a given period of time t, by formula:
J = C · i · t
The amount paid at the end of this investment must be given by the money invested plus the interest amount and is called amount (M). The amount is given by the expression:
M = C + J
M = C + C·i·t
M = C (1 + it)
The only concern we should have in relation to problems involving simple interest is with the rate and time units of measure, they must always be in equal units.
Example 4
Marta wants to invest R$6000 in a company that promises to generate profits of 20% a year under a simple interest regime. The contract made by Marta states that she can only withdraw the money after six months, determine what was the return on her money at the end of that period.
Observing the statement, see that the capital is equal to 6000, so we have C = 6000. The interest rate is 20% per year, and the money will be invested for six months. Note that the rate was given in the year, and the time in months, and we know that the unit of measure for both must be the same. Let's find the monthly fee, see:
We know that the rate is 20% per year, as a year has 12 months, so the monthly rate will be:
20%: 12
1.66% per month
0.016 per month
Replacing this data in the formula, we have to:
J = C · i · t
J = 6000 · 0.016 · 6
J = 96 · 6
J = 576 reais
Therefore, the amount to be withdrawn at the end of the six months is 576 reais, and the amount is:
M = 6000 + 576
M = 6576 reais
read more: Understanding the use of a çalculator ffinancial
Compound interest
In simple interest, the interest rate value is always calculated on top of the initial capital, the difference between these two systems (simple and compound interest) is precisely at this point, that is, in the way the rate is calculated. In compound interest, the interest rate is always calculated on top of the previous month's principal, this causes the interest to increase its value exponentially. THE formula to calculate the interest in the compound interest amortization system is given by:
M = C · (1 + i)t
On what M is the accumulated amount, Ç is the value of the initial capital, i is the interest rate given as a percentage, and t is the period in which the capital was invested in the system. As with simple interest, in the compound interest system, the rate and time must be in the same unit.
Example 5
Calculate the amount of the amount that Marta would collect at the end of the six months by applying her 6000 reais at an interest rate of 20% per year in the compound interest system.
(Given: 1.20,5 ≈ 1,095)
Note that the data is the same as in example 4, so we have to:
C = 6000
i = 0.2 p.a.
t = 0.5 years
Replacing the data in the compound interest formula, we have to:
M = 6000 · (1 + 0.2)0,5
M = 6000 · (1.2)0,5
M = 6000 · 1,095
M = 6572.67 reais
Therefore, the amount to be withdrawn by Marta in the simple interest system is 6572, 67 reais. Note that the amount in the compound interest system is greater than in the simple interest system, and this occurs in all cases. To better understand how this rate is calculated, visit: Fees çoppositeyou.

solved exercises
question 1 – (FGV – SP) A capital applied to simple interest, at the rate of 2.5% per month, triples by:
a) 75 months
b) 80 months
c) 85 months
d) 90 months
e) 95 months
Resolution
Alternative B.
We must find the time when the interest is equal to 2C, since, with the interest in this way together with the initially applied capital of C, we will have the amount of 3C (triple of the capital). Thus:
J = 2C; C=C; i = 2.5% per month; t = ?
J = C · i · t
2C = C · 0.025 · t

Thus, the time for this capital to triple is 80 months.
Note: 80 months equals 6.6 years.
question 2 – A commodity, after suffering an increase of 24%, had its price changed to 1041.60 reais. Determine the amount before adding.
Resolution
We can use the general addition formula to determine the value of the merchandise before the addition.
x · (1 + 0.01p)
In the formula, the value x is what we are looking for and p is the value of the addition, and this expression gives us the value of the product after the addition, hence:
1041.60 = x · (1 + 0.01p)
1041.60 = x · (1 + 0.01 · 24)
1041.60 = x · (1 + 0.24)
1041.60 = x · 1.24
See that we have an equation of the first degree, to solve it, we must isolate the unknown x, dividing both sides of the equality by 1.24, or, simply, pass the 1.24 dividing. Thus:
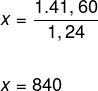
Therefore, the value of the merchandise before the addition was 840 reais.
by Robson Luiz
Maths teacher
A company deducts a certain percentage from its employees' annual salary for a private pension plan. The discount is p% on BRL 28,000.00 of annual income, plus (p + 2)% on the annual salary amount that exceeds BRL 28,000.00. João had a total discount of (p + 0.25)% of his annual salary for the private pension plan. João's annual salary, in reais, without the pension plan discount is:
a) 28,000.00.
b) 32,000.00.
c) 35,000.00.
d) 42,000.00.
e) 56,000.00.
The savings account had a yield of 0.68% and 0.54% in January and February 2009, respectively. A consumer price index, in those same months, was 0.46% and 0.27%, respectively. Determine, at the end of February 2009, the real gain from an investment in a savings account (gain from savings discounting inflation measured by the consumer price index) accumulated since January 2009.