Pyramids they are geometric figures that appear frequently, especially in architecture. the pyramids are Geometric solids built in space based on a polygon in the plane and a point outside that plane. As it is a three-dimensional figure, it is possible to calculate its volume, in addition, we can plan it and thus find its area.
Read more: Point, Line, Plane, Space: Basic Concepts of Spatial Geometry
What is Pyramid?
Consider a polygon withvexo contained in a plane and an H point that does not belong to the plane. We define the pyramid as being the union of all vertices of the convex polygon at point H.
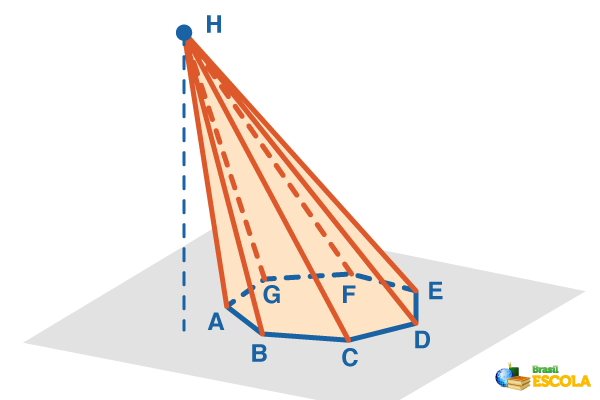
Elements of a Pyramid
Consider the pyramid below.
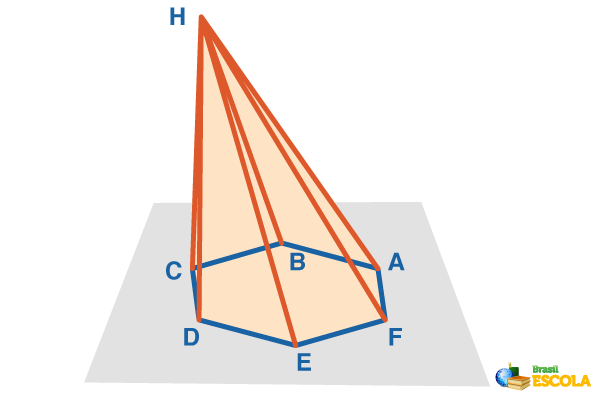
• Base of the pyramid: ABCDEF polygon.
• Pyramid apex: point H.
• Side faces: AHB, BHC, CHD, DHE, EHF and FHA, which are the triangles formed by the union of the vertex of the pyramid with the vertices of the polygon.
• Base edges: AB, BC, CD, DE, EF and FA, which are the sides of the base.
• Side edges: AH, BH, CH, DH, EH and FH, which are the segments of the side faces.
• Height of the pyramid: h, which is the distance between the apex of the pyramid and the base.
Let's establish the notations for some elements:
• A base area will be denoted by AB.
• The area of a side face will be represented by AF.
• The sum of face areas is called side area, and this is denoted by AL.
Thus, the total area of the pyramid is given by the sum of the base area (AB) with the side area (AL) and is denoted by AT, i.e:
THET = AB + AL
Know more: Trunk of the pyramid: know what it is and how to calculate your area
Types of Pyramids
The same way we name the prisms according to the base polygon, we also name the pyramids following this idea. For example, if a pyramid has a triangle, she is called triangular base pyramid, now, if a pyramid is based on a quadrilateral, is called quadrangular base pyramid, and so on.

Pyramids are also divided into two groups: straight and oblique. At pyramidsstraight are so called when the projection of the vertex coincides with the center of the base, otherwise they are said to be oblique. See the examples below:

If in a straight pyramid the base is a regular polygon, then the pyramid will be regular. In this type, the distance from the apex to the center of the base is the height of the pyramid.
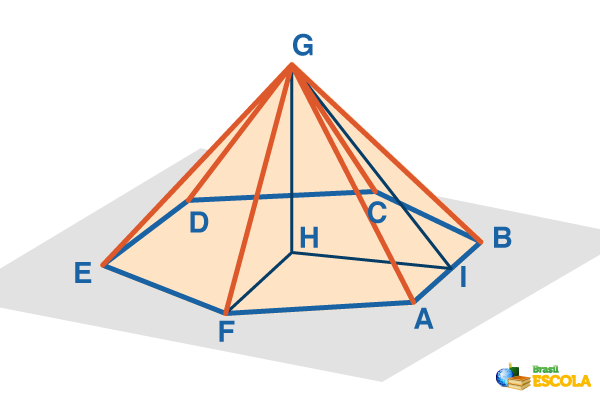
The segment that joins the apex of the pyramid with the midpoint of an edge of the base is called a apothema of the pyramid, in this case GI. The segment that joins the center of the base to the midpoint of an edge of the base is called apothema of the base, in this case HI.
Note the triangles GHI and GHF and note that they are right triangles, therefore, in it the Pythagorean theorem its valid. Thus:
(GI)2 = (GH)2 + (HI)2
(GF)2 = (GH)2 + (HF)2

Pyramid area
THE pyramid area is given by the sum of the side areas and the base area, that is:
THET = AB + AL
The non-existence of a specific formula is due to the fact that pyramids have different bases. In the previous expression, notice that the total area AT depends on the base area value. See some examples.
• Example
Calculate the total area of a straight pyramid, whose base is a square with a side 10 m and the height of a side face is equal to 13 m.
Solution
Initially we will draw the pyramid according to the exercise data.
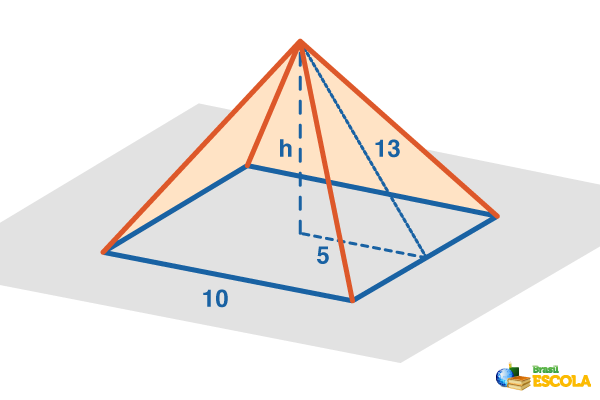
Note that we can calculate the face area with the given data using the triangle area formula.
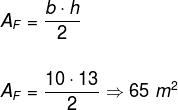
As we have four faces, the lateral area is equal to 65 · 4 = 260 m2.
Now, we must calculate the area of the base which is a square, so:
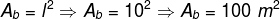
Therefore, the pyramid area is the sum of the side area and the base area.
THET = AB + AL
THET = 100+ 260
THET = 360 m2
Read too: fig areaflat ures: learn how to calculate different types
Pyramid volume
Consider a pyramid of height h.
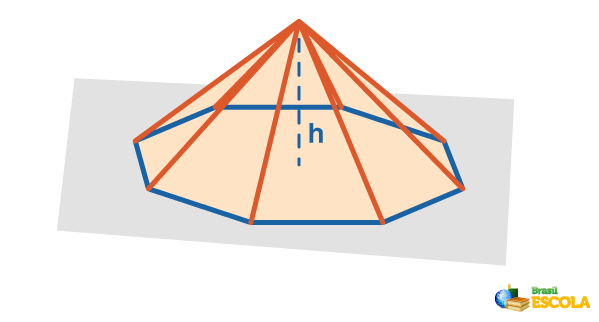
The volume of the pyramid is given by the third part of the product of the base area (AB) and height (h):
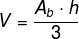
• Example
(Enem) Artur and Bernardo went camping and each took a tent. Both are shaped like a pyramid with a square base, with congruent side edges. Bernardo's tent is 10% higher in height and lateral edges than Arthur's. Thus, the ratio between the volumes of Bernardo and Arthur's tents, in that order, is:
The) 1,1
B) 1,21
ç) 1,331
d) 1,4641
and) 1,5
Solution
Initially, we will calculate the volume of Arthur's tent, denoted here by VTHE. Since the base of the pyramid is a square, its area is the measure of the squared side, let's represent it by L2.

Now let's determine the volume of Bernardo's tent, represented by VB. First, note that the height and edges are 10% higher compared to Arthur's tent, so we have to:
HB = h + 10% of h
HB = h + 0.1 · h
HB = 1.1 · h
Likewise for the base area:
THEB = (1,1)2 · L2
Therefore, Bernardo's tent area is:

As the objective of the exercise is to find the ratio between the volumes of Bernardo's and Arthur's tents, we have to:
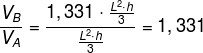
Realize that we can "cut" the fraction L2 · h over 3, as it represents the same number.
Alternative C
by Robson Luiz
Maths teacher

