Relation between parabola and coefficients of a function of the second degree

One high school function is a rule that relates each element of a set A to a single element of a set B and which can be written as follows:

f(x) = ax² + bx + c

You coefficients of a occupationofseconddegree are the numbers represented in this expression by the letters The, B and ç. The letter x is called variable.

All occupationofseconddegree can be graphically represented by a parable. Some of the features of this geometric figure can be related to the coefficients of the function of the second degree.
Coefficient A

O coefficientThe indicates the concavity of a occupationofseconddegree.

If a > 0, then the concavity of parable is facing up.

If a < 0, then the concavity of parable is facing down.

The following image shows a parable on the left that has concavity facing upwards and one on the right, with the concavity facing downwards.

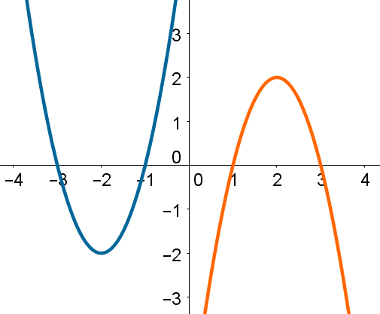
Thus, we can conclude that the coefficientThe at parable on the left is positive, and in the parable on the right it is negative.

In addition, the coefficient The it is also responsible for the “opening” of the parable. The higher the value of the

module of the coefficient, the smaller the aperture. To better understand this concept, look at points A and B on the parable Next:

The higher the value of the module of coefficientThe, the smaller the distance between points A and B.
Coefficient C

In a occupationofseconddegree, the coefficient C will always represent the meeting point of the y axis with the parable. Algebraically, you can notice this by setting x = 0 in a function of the second degree:

Do not stop now... There's more after the advertising ;)

f(x) = ax² + bx + c

f (0) = a0² + b0 + c

f (0) = c

Therefore, the point (0, c) is always part of the graph of any occupationofseconddegree and since x = 0, then that point is on the y-axis.

For example, the graph of the function f(x) = x² – 9 é:

Note that the meeting point of the y-axis with the graph of parable is the point (0, – 9). This rule is valid for all occupationofseconddegree.
Delta value (discriminating)

calculate the discriminating is the first step to be taken to find the roots of a occupationofseconddegree. Its value is found by substituting the coefficients of the second degree function in the formula:

∆ = b² – 4·a·c

The numerical value of ∆ indicates how many real roots a second-degree function has.

If ∆ > 0, the function has two distinct real roots.

If ∆ = 0, the function has a real root.

If ∆ < 0, the function has no real roots.

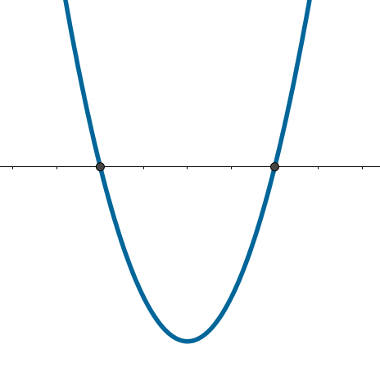
If this knowledge is combined with the coefficientThe of a occupationofseconddegree, we can find out a lot about a function. In the function f(x) = x² – 16, the value of ∆ in this function is:

∆ = b² – 4·a·c

∆ = 0² – 4·1·(– 16)

∆ = 4·16

∆ = 64

Also note that a = 1 > 0. So this function touches the x-axis twice and has the concavity facing up, which means its vertex is minimum point and will have a drawing similar to:

By Luiz Paulo Moreira
Graduated in Mathematics

Would you like to reference this text in a school or academic work? Look:

SILVA, Luiz Paulo Moreira. "Relation between parabola and coefficients of a function of the second degree"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/relacao-entre-parabola-coeficientes-uma-funcao-segundo-grau.htm. Accessed on June 28, 2021.