Type functions f (x) = y = ax + b, with a and b real numbers and to ≠ 0, are considered 1st degree. When represented on the Cartesian plane, they constitute a rising or falling line. And in the case of a = 0, the function is called a constant.
A function has points considered essential for the correct composition of its graph, and one of these points is given by the linear coefficient of the line represented in the function by the letter b, which indicates by which numerical point the line intersects the axis of ordinates (y).
In the following functions, note the numerical value of the linear coefficient and the graph representing the function:
y = x + 1
b = 1
Do not stop now... There's more after the advertising ;)

y = -x - 1
b = -1

y = 2x + 4
b = 4
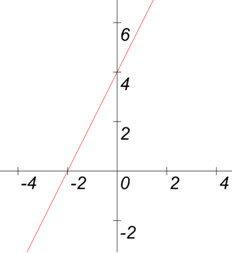
y = 2x – 4
b = – 4

y = 6x – 3
b = – 3

y = 5x
b = 0
by Mark Noah
Graduated in Mathematics
Brazil School Team
1st degree function - Roles- Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Linear Coefficient of a 1st Degree Function";
Brazil School. Available in: https://brasilescola.uol.com.br/matematica/coeficiente-linear-uma-funcao-1-o-grau.htm. Accessed on June 27, 2021.