THE generating fraction and the fractional representation of a periodic tithe. This representation is an important strategy in solving problems about basic Mathematics operations that involve periodic decimals. To find it, we can use equation techniques as well as a practical method.
Read too: How to solve operations with fraction?
What is a periodic tithe?
Before understanding what a generatrix fraction is, it is essential to understand what a periodic decimal is. There are two possible cases of periodic tithes: the simple periodic decimal and the compound periodic decimal. A periodic tithe is a decimal number that has infinite and periodic decimal part.

simple periodic tithe
The simple periodic decimal is composed of the integer part and the decimal part. THE decimal part is the repetition of your period, as shown in the examples below.
Examples:
a) 1.2222...
whole part → 1
decimal part → 0,2222…
Time course → 2
b) 3.252525...
whole part → 3
decimal part → 0,252525…
Time course → 25
c) 0.8888...
whole part → 0
decimal part → 0,8888
Time course → 8
Do not stop now... There's more after the advertising ;)
compound periodic tithe
A composite periodic decimal is a decimal that has an integer part, a decimal part, and, in its decimal part, a non-periodic part — known as the antiperiod — and the period.
Examples:
a) 2.0666...
whole part → 2
decimal part→ 0,0666…
Antiperiod → 0
Time course → 6
b) 13.518888...
whole part → 13
decimal part → 0,51888…
Antiperiod → 51
Time course → 8
c) 0.109090909...
whole part → 0
decimal part → 0,10909090
Antiperiod → 1
Time course → 09
Read too: What are equivalent fractions?
What is generative fraction?
generating fraction is the fractional representation of the periodic decimal, be it simple, be it composed. As the name suggests, the generating fraction generates the tithe when we share the numerator by the denominator of the fractional representation.
Examples:
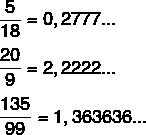
Step by step to calculate the generating fraction
Let's take a step-by-step look at the simple periodic decimal and the composite periodic decimal.
simple periodic tithes
To find the generating fraction of a simple periodic decimal, it is necessary to follow a few steps, namely:
1st step: equal the periodic decimal to x.
2nd step: according to the number of digits in the period, multiply both sides of the equation by:
10 → if there is 1 digit in the period;
100 → if there are 2 digits in the period;
1000 → if there are 3 digits in the period; and so on.
3rd step: calculate the difference between the equation found in step 2 and the equation equaled to x in step 1, and solve the equation.
Example 1:
Find the generating fraction of the 1,444 decimal…
x = 1.4444…
The period is 4 and, as there is only one digit in the period, we will multiply it by 10 of both sides:
10x = 1.444… · 10
10x = 14.444...
10x - x = 14.444.. – 0,444…
9x = 14
x = 14/9
So, the generating fraction of the tithe is:
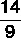
Example 2:
Find the generating fraction of the periodic decimal 3.252525…
x = 3.252525…
The period is 25 and, as it has 2 digits, we will multiply it by 100.
100x = 3.252525… · 100
100x = 325.252525...
Now calculating the difference between 100x and x:
100x - x = 325.2525... - 3.252525...
99x = 322
x = 322/99
So, the generating fraction of the tithe is:
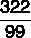
compound periodic tithe
When the periodic decimal is composed, what changes is that we added a new step in the resolution to find the generating fraction.
1st step: equal the periodic decimal to x.
2nd step: transform the compound periodic decimal into a simple periodic decimal by multiplying by:
10, if there is 1 digit in the antiperiod;
100 if there are 2 digits in the antiperiod; and so on.
3rd step: according to the number of digits in the period, multiply both sides of the equation by:
10 → if there is 1 digit in the period;
100 → if there are 2 digits in the period;
1000 → if there are 3 digits in the period; and so on.
4th step: calculate the difference between the equation found in step 3 and step 2, and solve the equation.
Example:
Find the generating fraction of the 5.0323232 tithe…
x = 5.0323232...
Note that there is 1 digit in the antiperiod, which is 0. We'll multiply it by 10 to make it a periodic decimal.
10x = 5.0323232... · 10
10x = 50.332232...
Now let's identify the period, which is 32. Since there are 2 digits, we will multiply the tithe by 100.
1000x = 5032.323232...
Now we calculate the difference between 1000x and 10x:
1000x - 10x = 5032.323232... - 50.323232...
990x = 4982
x=4982/990
So, the generating fraction is:

See too: How is a mixed number formed?
practical method
We use the practical method to facilitate the process of finding the generating fraction of the periodic decimal. Let's look at two different cases: when the periodic decimal is simple and when it is composite.
Practical method for simple periodic tithes
In a simple periodic decimal, the practical method is to:
1st step: write the sum between the integer part and the decimal part of the periodic decimal;
2nd step: transform the decimal part into fraction, as follows: the numerator will always be the period and the denominator will be:
9 → if there is 1 digit in the period;
99 → if there are 2 digits in the period;
999 → if there are 3 digits in the period; and so on.
3rd step: Sum the integer part with the found fraction.
Example:
5,888…
5,888… = 5 + 0,888…
By transforming 0.888... into fraction, we have numerator equal to 8, since 8 is the period of the fraction, and denominator equal to 9, since there is only 1 digit in the period, so:
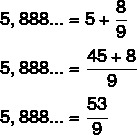
Practical method for periodic composite tithes
Example:
We will find the generating fraction of the 4,1252525 tithe…
First we identify the entire part, the antiperiod and the period of the composite tithe:
Whole part: 4
Antiperiod: 1
Period: 25
The numerator of the composite tithe is the difference between the number formed by the digits of the whole part, antiperiod and period, and the number formed by the whole part and antiperiod.
4125 – 41 =4084
In the denominator, for each number in the period, we add a 9 and then, for each number in the non-periodic part, a 0.
the period is 25, so we add 99; the antiperíall is 1, so we add 0, then the denominator é990.
The generating fraction of the tithe is:

solved exercises
Question 1 - When performing the division between two natural numbers, the periodic decimal 1.353535 was found… The generating fraction of this decimal is:

Resolution
Alternative C.
We will do x = 1.353535…
Multiplying by 100 on both sides, we have to:
100 x = 135.3535…
Now let's calculate the difference between 100x and x.

Question 2 - If x = 0.151515… and y = 0.242424…, is the division y: x equal to?
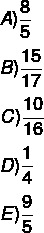
Resolution
Alternative A.
Finding the generating fractions by the practical method, we have to:
x = 0.151515…
The tithe has a period equal to 15, so its numerator is 15, and the denominator is 99.

With the same reasoning for y = 0.242424…, the numerator is 24, and the denominator is 99.

By Raul Rodrigues de Oliveira
Maths teacher


