When we are working with trigonometry and we come across an angle that is not found in the first quadrant, we can always reduce it in order to find the angle corresponding to this one that is precisely in the 1st quadrant. This is possible thanks to symmetry present in the trigonometric cycle. But we need to pay attention to what happens to the signs of the trigonometric functions in each quadrant.Let's see below some ways to work the quadrant shift in the trigonometric cycle.
Reduction to the First Quadrant
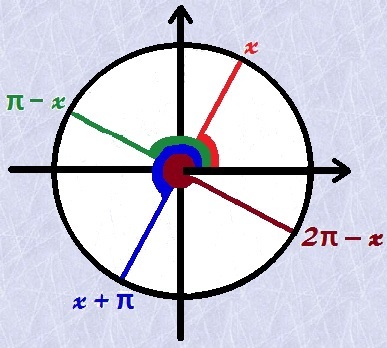
In the following figure, consider the angle x, highlighted in red in the first quadrant. We can find the angles that correspond to x in the other quadrants. The distance of these angles to x is always a multiple of 90°, such that the module of the trigonometric functions of these angles does not change.
Practical method for reduction to the first quadrant
If the angle we're working with is y and he is in second quadrant, its corresponding in the 1st quadrant will be the angle x such that π - x = y or 180° - x = y.
Example 1:
consider the angle 150°. To reduce it to the 1st quadrant, we will have the following:
180° - x = 150°
x = 30°
Analogously, if the angle y belong to third quadrant, Your correspondent x in the first quadrant will be given by x + π = y or 180° + x = y.
Example 2:
consider the angle 4π/3, your correspondent will be:
x + π = 4π3
x = 4π – π
3
x = π3
Finally, if the analyzed angle y belong to fourth quadrant, the angle x corresponding to it in the first quadrant will be given by 2π - x = y or 360° - x = y.
Example 3:
consider the angle 300°, reducing it to the first quadrant, we will have:
360° - x = 300°
x = 60°
Remember that the corresponding angles have similar values of sine, cosine and tangent, and the distinction occurs by the sign. At thefirst quadrant, the values of sine, cosine and tangent are positive. At the second quadrant, O sine is positive, while cosine and tangent are negative.. At thethird quadrant, sine and cosine are negative, while the tangent is positive. At the fourth quadrant, sine and tangent are negative, and cosine is positive.. We can see the distinction between the signs in the following image:

Check the signs of the trigonometric functions according to the quadrant
By Amanda Gonçalves
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/matematica/reducao-ao-primeiro-quadrante-no-ciclo-trigonometrico.htm