A relationship established between two sets A and B, where there is an association between each element of A with a single element of B through a formation law is considered a function. Look at the example:
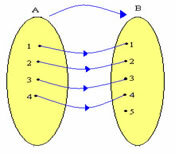
The study of functions is presented in several segments, according to the relationship between the sets, we can obtain innumerable formation laws. Among the studies of functions we have: 1st degree function, 2nd degree function, exponential function, modular function, trigonometric function, logarithmic function, polynomial function. Each function has a property and is defined by generalized laws. The functions have geometric representations in the Cartesian plane, the relationships between ordered pairs (x, y) are extremely important in the study of graphs of functions, as the analysis of the graphs generally demonstrates the solutions to the proposed problems using dependency relations, specifically, the functions.
Functions have a set called domain and another set called function image, in the Cartesian plane the x axis represents the domain of the function, while the y axis represents the values obtained as a function of x, constituting the image of the occupation.

An example of a function relationship can be expressed by a formation law that relates: the price to be paid as a function of the quantity of liters of fuel supplied. Considering the price of gasoline equal to R$ 2.50, we have the following formation law: f (x) = 2.50*x, where f (x): price to pay and x: quantity of liters. Look at the table below:
Note that for each value of x we have a representation in f(x), this model is a typical example of a 1st degree function.
by Mark Noah
Graduated in Mathematics
See more!
1st degree function
Definition and properties.
2nd degree function
Study of the Parable.


