In wave studies, we define periodic waves as being the waves generated by oscillating sources, that is, they are waves that are repeated at equal time intervals. In the figure above we have the basic representation of a periodic wave that propagates on a tensioned string. We can also see that we have some basic elements that are associated with it, such as crests and wave length, valleys and wave amplitude.
Let's now consider the figure below, where we have a tensioned string, that is, fully stretched. In the figure, we can identify the point as F the source emitting waves; and the point O as being the origin.

Based on the situation above, let's consider the time equal to zero (t = 0). In this case, the point F will perform a simple harmonic movement whose breadth is worth THE and the initial phase θ0, so the ordering y in F will vary over time. Following the MHS equation, we have:
y=A.cos (ω.t+ θ0 )
If no energy dissipation occurs during wave propagation, we can say that, after a certain time interval (Δt), the point
P situated in the middle of the rope begins to describe asimple harmonic movement with the same amplitude value THE, however late t about F.Like Δt is the time interval for the wave to reach P, we have:

In the equation above, x is the abscissa of the point P and v is the speed at which the wave travels along the string. Let's see the figure below:

So the generic point P have your salary, y, given as a function of time by:
y=A.cos[ω.(t-∆t)+θ0 ]
Remembering that ω = 2πf and that Δt = x/v, we have:
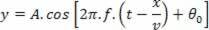
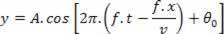
replacing  , Follow:
, Follow:
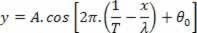
For each point on the string, the abscissa x is fixed and orderly y varies as a function of time, according to this function.
By Domitiano Marques
Graduated in Physics
Source: Brazil School - https://brasilescola.uol.com.br/fisica/onda-periodica-sua-equacao.htm
