Displacement and space traversed: what are exercises

Displacement and spacetraveled they are related but different physical quantities. While displacement is a vector physical magnitude, the space traveled is scalar. The displacement is the magnitude of the vector that connects the final and initial positions of a rover, while the space traveled is the sum of all linear displacements of a rover.

See too: Mechanics - area of ​​Physics that studies the movement of bodies

Displacement

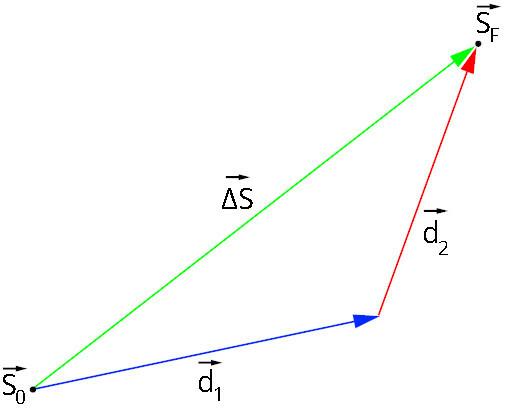
Displacement is a greatnessvector which can be calculated from the difference between two other vector quantities: the final position (S_F) and the starting position (S₀) of a piece of furniture. In other words, the displacement of a body equivalent to distancebetween these two positions, therefore, if this body moves and returns to the same position from which it started, its displacement will have been null.

Look at the figure below, where you can see two points, S_F and S_0. The arrow connecting these two points is what we call the vectordisplacement.

The red arrow, which connects A to B, is the displacement vector. In blue lines, you can see the space covered.

The displacement vector modulus (ΔS) tells us what is the distance between the start and arrival point of a rover. Such distance can be obtained by the values ​​of the components of the displacement vector. In the case of a displacement that occurs in two directions (x and y), the displacement vector modulus can be obtained from the Pythagorean theorem. The situation in this case is analogous to what we study in Mathematics for the distance between two points.

Another way to calculate is to add the different displacement vectors that give rise to the resulting displacement. In the figure below, we can see two arrows, d₁ and of₂, which represent two distinct displacements.

The vector sum of the displacements d₁ and of₂ is equivalent to the distance between the final positions (S_F) and initial (S₀).

Displacement formula

The formula used to calculate displacement is simple and consists of distance between two points.

s_F – final position

s₀ – starting position

Displacement can also be obtained using the Pythagorean theorem, if we already know the size of the x and y components of the displacement vector.

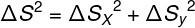
Lookalso:How to perform operations with vectors?

Do not stop now... There's more after the advertising ;)

space traversed

Space traveled is a scalar greatness, unlike displacement. The space or distance traveled is the sum of the modules of each rectilinear displacement that results in the total displacement of the body. In addition, the space traveled can be calculated by adding up all the distances the body travels to reach the final position. The space traveled is also often called displacementclimb.

See too: Tips for solve kinematics exercises

Exercises on displacement and space traversed

Question 1 — To carry out his morning deliveries, a newspaper delivery person moves according to the figure below. Each of the squares represents a court, whose side is equal to 150 m.

Determine the distance traveled by the postman and his total displacement, in approximate values.

a) 450 m and 450 m

b) 450 and 474 m

c) 150 m and 300 m

d) 300 m and 150 m

Resolution:

To find the space covered, just add the sides of the blocks that the postman covered, which results in 450 m. Displacement, in turn, requires us to calculate the hypotenuse of the triangle in the figure, which coincides with the magnitude of the displacement vector. For that, we use the Pythagorean theorem:

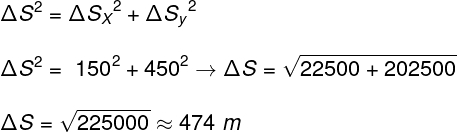
Based on the calculation, the correct answer for this exercise is the letter B.

Question 2 — A Formula 1 car travels a closed circuit whose length is 5.5 km. Knowing that, during a complete race, the car completes 20 laps on this track, determine the space traveled and the displacement of that vehicle during a complete race.

a) 0 km and 110 km

b) 110 km and 0 km

c) 55 km and 55 km

d) 0 km and 55 km

Resolution:

The total space covered by the Formula 1 car is 110 km, as it completes 20 laps on a 5.5 km track. The displacement, in turn, is null, since the car returns to the same place where the race started, so the correct alternative is the letter B.

By Rafael Hellerbrock
Physics teacher

Would you like to reference this text in a school or academic work? Look:

HELERBROCK, Rafael. "Displacement and space traversed"; Brazil School. Available in: https://brasilescola.uol.com.br/fisica/deslocamento-e-espaco-percorrido.htm. Accessed on June 27, 2021.