When obtaining any sample of size n, the sample arithmetic mean is calculated. Probably, if a new random sample is taken, the obtained arithmetic mean will be different from that of the first sample. The variability of means is estimated by their standard error. Thus, the standard error evaluates the accuracy of the calculation of the population mean.
The standard error is given by the formula:
Where,
sx → is the standard error
s → is the standard deviation
n → is the sample size
Note: The better the precision in calculating the population mean, the smaller the standard error.
Example 1. In a population, a standard deviation of 2.64 was obtained with a random sample of 60 elements. What is the likely standard error?
Solution: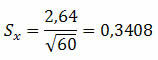
This indicates that the average can vary 0.3408 more or less.
Example 2. In a population, a standard deviation of 1.32 was obtained with a random sample of 121 elements. Knowing that an average of 6.25 was obtained for this same sample, determine the most likely value for the average of the data.
Solution: To determine the most likely mean value of the data we must calculate the standard error of the estimate. Thus, we will have:

Finally, the most likely value for the average of the data obtained can be represented by:
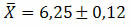
By Marcelo Rigonatto
Specialist in Statistics and Mathematical Modeling
Brazil School Team
Statistic - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/erro-padrao-estimativa.htm
