The study about numerical sets constitutes one of the main areas of mathematics, since they are very important for the theoretical development of the area and have several practical applications. Numerical sets comprise in studying:
- natural numbers;
- integers;
- rational numbers;
- irrational numbers;
- real numbers; and
- complex numbers.
read more: Prime numbers - numbers that have only 1 and themselves as divisors
Set of natural numbers
The development of the first civilizations brought with it the improvement of agriculture and commerce and, consequently, the using numbers to represent quantities. The first set came naturally, hence its name. The natural named set is used to represent quantities, it is denoted by the symbol ℕ and is written in sequence form. Look:

O set of numbers naturais é infinite and closed for operations of addition and multiplication, that is, whenever we add or multiply two natural numbers, the answer is still natural. However, for subtraction operation and division, the set is not closed. Look:
5 – 6 = –1
3 ÷ 2 = 0,5
Note that the numbers –1 and 0,5 they do not belong to the set of naturals, and this is the justification for the creation and study of new sets of numbers.
Do not stop now... There's more after the advertising ;)
Also, placing an asterisk (*) in the symbol of the natural set, we must remove the number zero from the list, see:
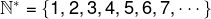
whole numbers set
The whole number set came up with the need to carry out the operation of subtraction no restrictions. As we have seen, when a smaller number is subtracted from a larger one, the answer does not belong to the group of naturals.
The set of integers is also represented by an infinite numerical sequence and is denoted by the symbol ℤ.
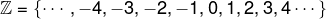
As in the set of natural numbers, by placing an asterisk in the symbol ℤ, the element zero is removed from the set, like this:
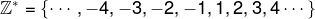
The (–) symbol that accompanies a number indicates that it is symmetric, so the symmetric of the number 4 is the number –4. Also note that the set of natural numbers is contained in the set of whole numbers, that is, the set of natural numbers is a subset of the set of whole numbers.
ℕ ⸦ ℤ
Read too: Operations with integers – what are they and how to calculate?
set of rational numbers
O set of rational numbers é represented by the symbol ℚ and is not represented by a numerical sequence. This set is made up of all the numbers that can be represented as a fraction. We represent its elements as follows:
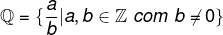
We know that every whole number can be represented by a fraction, that is, the set of whole numbers is contained in that of rational numbers, so, the set of integers is a subset of the rationals.
ℕ ⸦ ℤ ⸦ ℚ
Numbers that have infinite representation, such as periodic tithes, also have representation in the form of a fraction, thus they are also rational.
Read too: Operations with fractions - step by step how to solve them
Set of irrational numbers
As we have seen, a number is rational if it can be written as a fraction. It has also been said that infinite and periodic numbers are rational, however, there are some numbers that cannot be written in the form of a fraction and which, therefore, do not belong to the set of rational numbers.
These non-rational numbers are called irrational and its main characteristics are the infinity of the decimal part and non-frequency, that is, no number in the decimal part is repeated. See some examples of irrational numbers.
- Example 1
The square roots of numbers that are not perfect squares.

- Example 2
Constants coming from special reasons like gold number, Euler number or Pi.
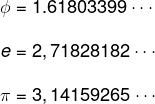
Set of real numbers
O set of real numbers is represented by the symbol ℝ and is formed by the unityof the set of rational numbers with the set of irrational numbers. Remember that the set of rationals is the union of natural and integer sets.

When we arrange the real numbers on a line, we have that the number zero is the origin of the line, to the right of zero will be the positive numbers, and to the left, the negative numbers.

As this axis is real, we can say that between two numbers there are infinite numbers and also that this axis is infinite both in the positive direction when in negative direction.
Set of complex numbers
O complex number set it's the last and it arose for the same reason as the set of integers, that is, it is an operation whose development only with the set of reals is not possible.
Solving the following equation, see that it has no solution, knowing only the real numbers.
x2 + 1 = 0
x2 = –1
Note that we have to find a number that when elevatedO squared, results in a negative number. We know that any number squared is always positive, therefore, this calculation has no real solution.
Thus were created the complex numbers, in which we have a imaginary number denoted by i, which has the following value:

So, realize that the equation that before had no solution now has it. Check out:
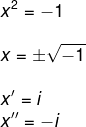
read more: Properties involving complex numbers
actual intervals
In some cases, we will not use every real axis, that is, we will use parts of it that will be called breaks. These intervals are subsets of the set of real numbers. Next, we will establish some notations for these subsets.
Closed range - without including the extremes
An interval is closed when it has its two extremes, that is, the minimum and maximum, and, in this case, the extremes do not belong in the range. We will denote this using an open ball. Look:

In red are the numbers that belong to this range, that is, they are numbers larger than a and smaller than b. Algebraically we write such an interval as follows:
the < x
Where the number x is all the real numbers that are in this range. We can also represent it symbolically. Look:
]The; B[ or (The; B)
Closed range - including extremes
Now let's use closed balls to represent that the extremes belong to the range.

So we're collecting real numbers that are between a and b, including them. Algebraically we express such an interval by:
the ≤ xb
Using symbolic notation, we have:
[The; B]
Closed range - including one of the extremes
Still dealing with closed intervals, we now have the case where only one of the extremes is included. Therefore, one of the marbles will close, indicating that the number belongs to the range, and the other does not, indicating that the number does not belong to that range.

Algebraically we represent this range as follows:
the ≤ x
Symbolically we have:
[The; B[ or [The; B)
Open range - no end inclusion
A range is opened when does not have a maximum or minimum element. Now we will see an open range case that has only maximum element, which is not included in the range.

See that the range consists of real numbers less thanB, and also note that the number b not belonging to the range (open ball), so, algebraically, we can represent the interval by:
x
Symbolically we can represent it by:
] – ∞; B[ or (– ∞; B)
Open range - including the extreme
Another example of an open range is the case where the extreme is included. Here we have a range in which the minimum element appears, see:

Note that all real numbers are greater than or equal to the number a, so we can write this range algebraically by:
xto
Symbolically we have:
[The; +∞[ or [The; +∞)
open range
Another case of open range is formed by numbers larger and smaller than the numbers fixed on the real line. Look:

Note that the real numbers that belong to this range are the ones less than or equal to the number a, or the ones that are greater than the number b, so we have to:
x to orx > b
Symbolically we have:
] – ∞; a] U ] b; + ∞[
or
(– ∞; a] U(b; + ∞)

by Robson Luiz
Maths teacher



