It is known as a rational number every number that can be represented as an irreducible fraction. Throughout human history, the idea of number has been gradually developed in accordance with human needs. The representation of numbers in fractions, for example, solved problems that were solved only with whole numbers.
A rational number can be represented from a fraction, so there are methods to transform whole numbers, decimal numbers exact and periodic decimals in fractions.
Read too: Operations with fractions – how to solve?
What are rational numbers?
The rational numbers are an expansion of the set of whole numbers, then, in addition to the whole numbers, were added all fractions. O set of the rational numbers is represented by:

What this representation says is that a number is rational if it can be represented as the fraction The about B, such that The is an integer and B is a non-zero integer. But if we are to define rational numbers less rigorously, we can say the following:
Rational numbers are all numbers that can be represented as a fraction. |
Meet this definition:
you integerss, for example: -10, 7, 0;
you exact decimal numbers, for example: 1.25; 0,1; 3,1415;
at simple periodic tithes, for example: 1.424242…;
at compound periodic tithes, for example: 1.0288888…
No are rational numbers:
At non-periodic tithes, for example: 4,1239489201…;
At rootsnot exact, for example:
 ;
;- THE frogiz square of negative numbers, for example:
 .
.
Observation: The existence of non-rational numbers causes other sets to emerge, such as irrational numbers and complex numbers.
Do not stop now... There's more after the advertising ;)
Representation of rational numbers
Understanding that the fraction is a division of two whole numbers, to be a rational number, you can represent this number as a fraction. Therefore, each of the cases mentioned above as rational numbers (whole numbers, exact decimals, and periodic decimals) can be represented as a fraction.
integers
There are infinite possibilities for representing an integer as a fraction, as a fraction can be represented in irreducible form or not.
Examples:

exact decimals
To turn an exact decimal number into a fraction, we count the number of numbers in its decimal part, that is, after the decimal point. If there is a number after the comma, we will write the integer part plus the decimal part without the comma over 10. If there are two numbers in the decimal part over 100, in practice, the amount of numbers in the decimal part will be the amount of zeros we have in the denominator. See the example:
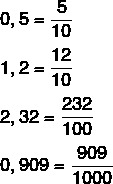
periodic tithes
Finding the fractional representation of a tithe is not always an easy task, what we call generating fraction. To facilitate this work, it was observed that, in the equation we used to find the generating fraction, there are regularities, which allowed the development of a practical method.
First, we need to understand that there are two types of periodic tithes, simple and compound. One tithe is simple if, in its decimal part, there is only the part that is repeated, that is, the period. One tithe is compound if, in its decimal part, there is a non-periodic part.
Example:
9,323232… → simple periodic decimal
Integer part equals 9.
Period is equal to 32.
8,7151515… → compound periodic tithe
Integer part equals 8.
Non-periodic decimal part is equal to 7.
Period is equal to 15.
See too: Equivalent fractions - fractions that represent the same amount
→ 1st case: generating fraction of a simple periodic decimal
In the first case, to turn a simple periodic decimal into a fraction by the practical method, just write the entire part plus the period without the comma in the numerator. In the denominator, for each element in the periodic part, we add a 9.
Example:
The generating fraction of 9.323232…, as we have seen, has a period equal to 32, that is, two numbers in its period, so the denominator is 99. The integer part plus the periodic part without the comma is 932, which is the numerator. So, the generating fraction of this tithe is:
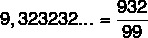
→ 2nd case: generating fraction of a composite periodic decimal
The periodic composite tithe is a little more laborious. Let's find the generating fraction of the tithe we worked on in the example.
8,7151515… → compound periodic decimal.
Integer part equals 8.
Non-periodic decimal part is equal to 7.
Decimal part of the period is equal to 15.
The numerator will be the subtraction 8715 – 87, that is, the difference between the number that goes from the whole part to the periodic part with the non-repeating part of the tithe.
The numerator will be equal to 8715 – 87 = 8628.
To find the denominator, let's analyze the decimal part. First let's look at the non-periodic and periodic decimal part. In this case, the decimal part of the number is 715. For each number that is in the periodic part, let's add a 9 at the beginning of the denominator. Since the periodic part in this case has two numbers (15), there will be two 9s in the denominator. For each number in the decimal part that is not periodic, we will add a 0 at the end of the denominator, which will be 990.
Soon, the generating fraction of the tithe will be:


Properties of rational numbers
Between two rational numbers, there will always be another rational number
It is interesting to think about this property, which was much discussed by ancient peoples, becoming a paradox. Choosing two rational numbers, there will always be a number between them.
Example:
Between 1 and 2, there is 1.5; between 1 and 1.5, there is 1.25; between the 1 and the 1.25, there is the 1.125 and so on. As much as I choose two rational numbers with very little difference between them, it is always possible to find a rational number between them. This property makes impossible to define successor and predecessor in rational numbers.
The four operations on the set of rational numbers are closed
We say that the set is closed for the sum, for example, if the sum of two rational numbers always generates another rational number as an answer. This is what happens with the four operations on Q.
THE addition, subtraction, division and multiplication between two rational numbers will always result in a rational number. In fact, even the potentiation of a rational number will always generate a rational number in response.
The set of rational numbers is not closed to the radiciation. Thus, msince 2 is a rational number, the square root of 2 is a irrational number.
See too: Equivalent fractions - fractions that represent the same amount
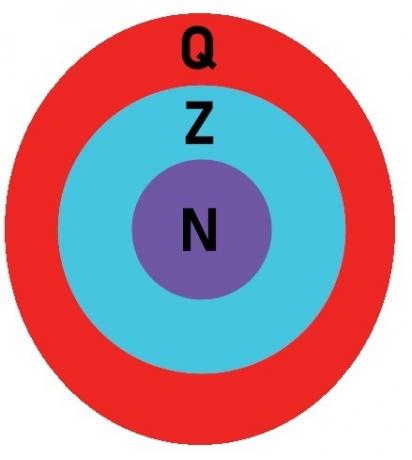
Subsets of rational numbers
We know how subsets or inclusion relation the sets formed by elements that belong to the set of rational numbers. There are several possible subsets, as the set of whole numbers or natural, since every whole number is rational, just as every natural number is rational.
Example:
Set of integers: Z= {…-3, -2, -1, 0.1, 2, 3, …}.
When that happens, we say that Z ⸦ Q (It reads: Z is contained in Q or the set of whole numbers is contained in the set of rational numbers.)
There are some symbols that are essential for creating subsets of Q, they are: +,- and *, which mean, respectively, positive, negative and non-null.
Examples:
Q* → (reads: set of non-zero rational numbers.)
Q+ → (reads: set of positive rational numbers.)
Q- → (reads: set of negative rational numbers.)
Q*+ → (reads: set of positive and non-zero rational numbers.)
Q*- → (reads: set of negative and non-zero rational numbers.)
Note that all these sets are subsets of Q, as all elements belong to the set of rational numbers. In addition to the sets presented, we can work with several subsets in Q, such as the set formed by odd numbers, or cousins, or pairs, finally, there are several and several possibilities of subsets.
By Raul Rodrigues de Oliveira
Maths teacher