Operations with decimal numbers they are very present in everyday life. The decimal numbers, which are part of the set of rational numbers, their main characteristic is the representation of their elements in the form of a fraction, that is, every number that can be written in the form of a fraction is a decimal number. As we well know, this numerical set has the four well-defined basic operations: addition, subtraction, multiplication and division.
Know more: Operations with sets: what are they and how to do it?
Nomenclature of decimal numbers
In order to facilitate the definitions to come, below we establish some nomenclatures. One decimal number is formed by its integer part and the decimal part. The decimal part is arranged as follows: tenth, hundredth, thousandth, tenth of a thousandth, hundredth of a thousandth, and so on.
See the example:

Addition with decimal numbers
Adding decimal numbers is defined similarly to adding whole numbers in this operation. we must add whole part to whole part, tenths to tenths, hundredths to hundredths, and so on successively. In other words, we must
put comma below comma, see the example.Example 1
Let's determine the sum of the numbers 0.65 and 0.792. Remember: the number 0 at the end of any decimal number does not add value.

Example 2
Determine the value of the sum 1.442 + 2.4.


Subtraction with decimal numbers
The subtraction between two decimal numbers is done in the same way as their addition, we operate whole part with whole part, tenths with tenths, and so on. See the examples.
Example
Determine the difference between the numbers 3.842 and 1.442.

Multiplication with decimal numbers
The multiplication between two decimal numbers can be performed in two ways: we can operate in a similar way to multiplication of two whole numbers, adding, at the end, the number of decimal places of the two numbers and placing them in the result; or we can turn the decimal numbers into fractions and use the fraction multiplication.
Do not stop now... There's more after the advertising ;)
Let's remember how to transform decimal number into fraction?Decimal to Fractional Number TransformationTo write a decimal number in its fractional form, we must keep the decimal number without the comma in the fraction numerator, and in the denominator we put the power of 10 according to the number of decimal places we "walk" to make the decimal number into whole. See the examples. Example 1 Let's write the number 0.43 as a fraction. For the comma to disappear, we must “walk” two decimal places, that is, we need to multiply the number by 100. Thus: 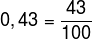 Example 2 To write the number 0.8 in its fractional form, we must walk one decimal place, therefore: 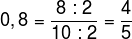 |
Example
Using both methods, determine the product between 0.42 and 1.2. Before performing the multiplication, notice that 0.42 has two decimal places and the number 1.20 has two of them. The sum of this results in four decimal places, that is, the result must have four decimal places.

That is, 0.42 x 1.2 = 0.504.
Now, transforming the numbers to their fractional form, we have the following multiplication:

Read too: Fraction simplification: learn how to do it
division with decimal numbers
In dividing decimal numbers we will also look at two methods that can be considered equivalent. The first method is to "walk" the same number of decimal places, that is, multiply by powers of 10 until the comma is no longer present. The second method is to represent the numbers as a fraction and perform the division of fractions.
Example
Let's perform the division between the numbers 0.504 and 1.2.
With the first method, we must multiply the dividend and divisor by the same number until the comma disappears.
In order for the comma to disappear from the denominator, we must multiply it by 1000, so we will do the same with the divisor.
0,504 · 1000 = 504
1,2 · 1000 = 1200
Setting up the account, we have:

Turning decimal numbers into fractions, we have:
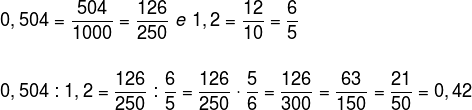
by Robson Luiz
Maths teacher



