According to Newton's Second Law, when we apply a force to an object that contains mass, it acquires acceleration. For a body in circular motion, that is, for a body in rotation, we can determine its position and velocity as a function of variables such as angle and angular velocity, in addition to the radius of the trajectory.
Let's see the figure above, in it we have a mass body m which is attached to a central axis, which rotates in a circular path whose radius is worth R. Let's analyze this movement. Still referring to the figure above, suppose that a force of intensity F always act in the direction of tangential velocity v of the body of mass m. We can write Newton's Second Law for the modulus of quantities:

As the linear velocity of a circular motion is given by v = ω.R, we can write the above equation as follows:
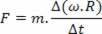
Multiplying both sides by R, we will have:
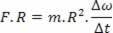
Knowing that the quotient between angular velocity and time gives us the angular acceleration, we have:
F.R=m. R2.α
Remembering that the force is perpendicular to the radius of the trajectory, we see that
F.R = M is the modulus of the torque exerted by the force F in relation to the center of the circular movement. We have as a result:M = m. R2.α ⟹ M = I.α
Where I = m. R2.
the equation M = I.α lists the torque modulus M with the angular acceleration α and with the amount I which represents the rotational inertia of the object. The amount I is known as the moment of inertia of the body and its unity in the SI is kg.m2.
In this example, we came to the conclusion that the moment of inertia it is related to both the mass and the radius of the circular path. The moment of inertia equation allows you to calculate the moment of any body, so we can say that the moment of inertia equation (M = I.α) is equivalent to Newton's Second Law for objects subject to torque.
By Domitiano Marques
Graduated in Physics
Source: Brazil School - https://brasilescola.uol.com.br/fisica/sistema-rotacao-momento-inercia.htm