Calculating the pressure in a body immersed in a fluid.

In this article we will look at how we can calculate the internal pressure in a fluid. Remembering that a fluid is a set of substances in which the internal cohesion forces between its constituents are quite small.

Let's assume we have a fluid in balance. In this case, for a fluid in equilibrium, the sum of the forces acting on it is equal to zero. Let's see the figure above, where we have a cube on its side L. According to the figure, we can conclude that the forces acting on it are equal to zero, that is, adding F₁ and F₂ we will result in a value of zero.

We can also see that on each face of the cube from the side L a pressure exerted by the liquid acts. We will call this pressure P. In this way, on the upper face the pressure is valid P₁, and on the underside it is worth P₂. Pressures on the hub are exerted by liquid external to the hub and result in forces that are directed into the hub. Therefore, F₁ points down and F₂ points up.

the F force₁ exerted on the upper face depends on the pressure P₁ and the area of ​​the top face of the cube. So we have:

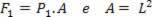
Similarly, pressure P₂ exerts a total upward force equal to:

As the cube is in equilibrium, that is, it does not go up or down, we can write that:

Or we can write:

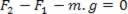
In this relationship above, we have to m.g is the weight of the cube and can be calculated from its density. d = m/V and its volume V = L³:

Like

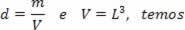
Substituting in I, we have:

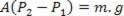
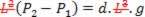
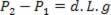
This result shows that the pressure difference between two points inside the liquid depends on the density of the liquid and the vertical distance between them, which in this case is L.

If we imagine that the pressure on the surface of the liquid is P_O, we can write the pressure at any depth H (L = h) like:

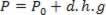
realize that H is the measure of depth at which we are calculating the pressure, and that P_O it is the pressure on the surface of the liquid, exerted by external agents such as the atmosphere.

By Domitiano Marques
Graduated in Physics

Source: Brazil School - https://brasilescola.uol.com.br/fisica/calculando-pressao-um-corpo-imerso-um-fluido.htm