O prism it is a geometric solid studied in spatial geometry. He has two parallel bases and formed by polygons, and its lateral faces are always parallelograms. The prism is named according to the shape of its base. If the base is a pentagon, for example, it will be a prism with a pentagonal base.
There are two possible classifications for the prism, which is the straight prism, when it has lateral edges perpendicular to the base, and the oblique prism, when the side edge is not perpendicular to the base. To calculate the total area and volume of a prism, we use specific formulas.
Read too: What are the differences between flat figures and spatial figures?
prism elements
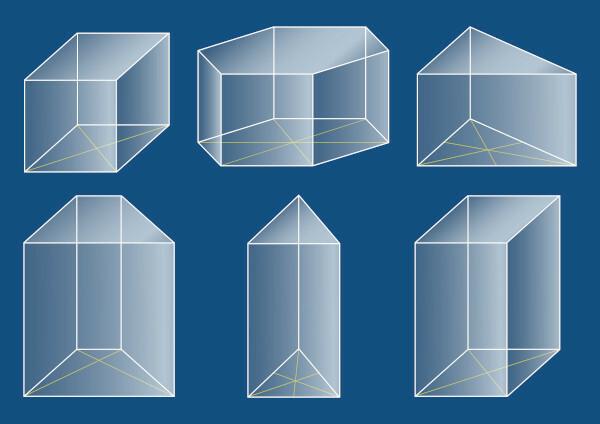
At spatial geometry, geometric solids are classified as polyhedra when they have all their faces formed by polygons. O prism, which is a particular case of polyhedron, has two parallel bases, shaped like any polygon, and side faces formed by parallelograms. The main elements of a prism are, like the other polyhedra:
- the faces,
- the vertices and
- the edges.

In a prism, faces are the polygons that form the geometric solid. Edges are line segments formed by the meeting of two faces, and vertices are points.
Do not stop now... There's more after the advertising ;)
prism bases
In a prism, identifying its base is of great importance, as it is how we can differentiate one prism from another. If the base of the prism is triangular, for example, it is known as a prism with a triangular base; if it is pentagonal, base pentagonal prism, and so on. É through the polygon which forms the basis of the prism, therefore, that we can differentiate it.

According to the base, the prism can be named as:
- triangular prism: has each of the bases in the format of a triangle;
- quadrangular prism: has each of the bases in the format of a quadrilateral;
- pentagonal prism: it has each of the bases in the shape of a pentagon;
- hexagonal prism: has each base in the shape of a hexagon;
- octagonal prism: has each of the bases in the shape of an octagon.
Read too: What are Plato's solids?
prism classification
There are two possible classifications for a prism: it can be straight, when the side faces form a right angle with the bases, and can be oblique, if the base does not make a right angle to the base.

Total prism area
The total area of a polyhedron is nothing more than the sum of area of all prism faces. In a prism, to find the total area, it is important to consider what the shape of your base is.
Be theB the area of the base of a prism. We know that it has two bases and side areas, which are always parallelograms. So be Sthere = Al1 + Al2 … THEln the sum of the side areas. The total area of any prism is calculated by:
THET = 2AB + Sthere
prism volume
To find the prism volume, there is a formula that it also depends on the base format of the prism. The volume of any prism can be calculated by:
V = AB · H
Example:
The prism below has a quadrangular base. Knowing that its base is a square with sides that measure 3 centimeters and that the height is 8 centimeters, so what is the total area and volume of this prism?

We know that the area of square is equal to the squared side, so:
THEB = l²
THEB = 3²
THEB = 9 cm²
The side areas are all congruent and have the shape of a rectangle of sides with 3 cm and 8 cm. In addition, you can see that there are 4 rectangles that form the lateral area of this prism, like this:
THEthere = b · h
THEthere = 3 · 8
THEthere = 24 cm²
As there are 4 congruent rectangles in the side area, so:
sthere = 4 · 24 = 96 cm²
The total area of this prism is calculated by:
AT = 2Ab + Sl
AT = 2·9 + 96
AT = 18 + 96
AT = 114 cm²
Now let's calculate the volume:
V = AB · H
V = 9 · 8
V = 72 cm³
See too: What are geometric shapes?
solved exercises
Question 1 - (FEI) From a wooden beam with a square section of side l = 10 cm, a wedge of height h = 15 cm is extracted, as shown in the figure. The volume of the wedge is:

A) 250 cm³
B) 500 cm³
C) 750 cm³
D) 1000 cm³
E) 1250 cm³
Resolution
Alternative C.
Since the base is a triangle, we know that:
THEB =(b · h): 2
THEB = (10·15 ): 2
THEB = 150: 2
THEB = 75 cm²
Now let's calculate the volume:
V = AB · H
V = 75 · 10
V = 750 cm³
Question 2 - About prisms, judge the following statements.
I – The cylinder is a prism that has circular bases.
II – Every polyhedron is a prism, as both have faces formed by polygons.
III – A prism with a triangular base has 6 vertices, 5 faces and 9 edges.
They are correct:
A) only statement I.
B) only statement II.
C) only statement III.
D) only statement I and III.
E) All statements are correct.
Resolution
Alternative C.
I → False, because the cylinder it has a circular base, and the circle is not a polygon, so the cylinder is not a prism.
II → False, because every prism is a polyhedron, but there are polyhedra that are not prisms.
III → True.
By Raul Rodrigues de Oliveira
Maths teacher
Would you like to reference this text in a school or academic work? Look:
OLIVEIRA, Raul Rodrigues de. "Prism"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/prisma-1.htm. Accessed on June 27, 2021.



