The studies referring to angles on the circumference helped and still help the plane geometry. With applications in astronomy and in other areas of knowledge, this study was deepened and developed different relationships and properties for each of the cases. The cases are:
- central angle;
- inscribed angle;
- inner angle;
- internal eccentric angle;
- external eccentric angle;
- segment angle.
For each case, there are specific properties that relate the arc of the circle to the angle.
Read too: What are the differences between circle and circumference?

elements of the circle
THE circumference has important elements for understanding this geometric shape. We know as a circle the set of points that are equidistant from the point C, known as the center.
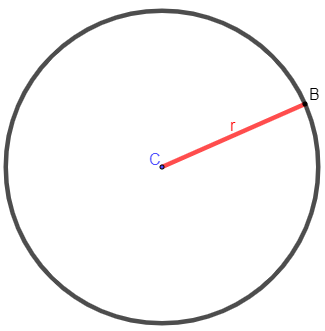
C → center
r → radius
In addition to the center and radius, the circumference also has as an important element the rope, which are the segments that connect one end of the circle to the other.
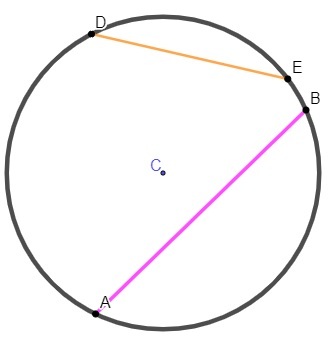
When this string passes through the center, it is known as diameter. The diameter of a circle has a length equal to the length of two radii and is a special case of rope.
Circumference angle cases
The studies of angles on the circumference they relate the arcs formed by the angles to the angle itself.
Do not stop now... There's more after the advertising ;)
center angle
Occurs when the angle is at the center of the circle. When this happens, we can say that the central angle amplitude equals arc amplitude.

Example:
Calculate the value of arc d.
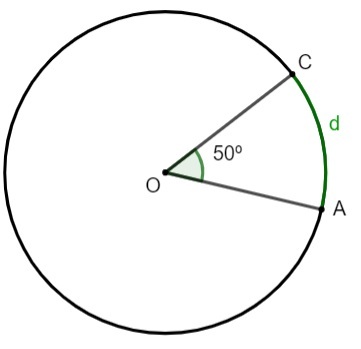
Since the central angle is equal to 50°, the amplitude of the arc denoted by d is also 50°.
See too: How to find the center of a circle?
Angle inscribed on the circumference
An angle is known as an inscribed when its vertex is a point on the circumference. When this occurs, the amplitude of the arc is equal to half the angle measurement.
Example:
Calculate the value of α in the image.
The arc is equal to twice the angle, that is, to find the value of α, just divide 72 by 2.
α = 72º: 2
α = 36º
Inner eccentric angle
An angle is known as an inner eccentric. when it's not at the center of the circumference, but it is located on the inner part of the circle and cannot be an inscribed angle. When this happens, we can define two arcs. The angle will be the arithmetic average between them, that is, the sum divided by two.

Example:
Calculate the value of the angle α on the circle knowing that C is not the center of the circle.
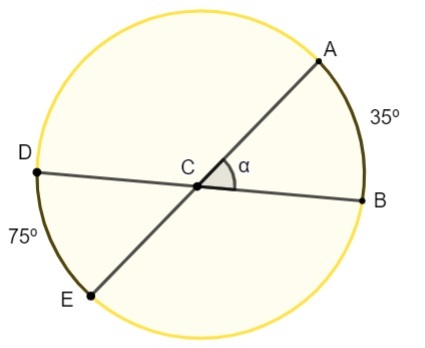

Also access: How to build circumscribed polygons?
External eccentric angle
We know as external eccentric the angle that is outside the circumference. When this happens, it forms two arcs, and the angle value is calculated by half the difference between the larger arc and the smaller arc.

Example:
Calculate the value of angle α.


segment angles
The angle is known as the segment angle when it is shaped by a tangent line segment à circumference and the other not. When this occurs, the angle is equal to half of the arc.
Example:
What is the value of the angle α on the following circle?
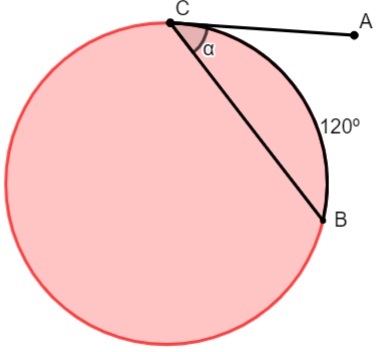
Analyzing the image, we know that the angle α is equal to half of the arc, that is, half of 120º, so α = 60º.
See too: Calculations and formula of the reduced equation of the circle
solved exercises
Question 1 - We can say that the value of the angle BÂC in the following triangle is:

A) 60th
B) 65th
C) 70th
D) 75th
E) 90º
Resolution
Alternative B.
Analyzing the circle, the arc formed by the points AB has an amplitude equal to the half circle, or that is, 180°. Since angle C is inscribed, then it corresponds to half of 180°, so angle C is equal to 90º.
The sum of the triangle's internal angles is always equal to 180º, so we have to:
25º + BÂC + 90º = 180º
BÂC = 180º - 90º - 25º
BÂC = 90º - 25º
BAC = 65º
Question 2 - Calculate the value of x on the following circle.

A) 10
B) 15th
C) 20th
D) 40th
E) 45th
Resolution
Alternative C.
Knowing that AÔB is the central angle and that it corresponds to the value of the arc, then we have to:
2x + 5th = 45th
2x = 45th - 5th
2x = 40th
x = 40º: 2
x = 20th
By Raul Rodrigues de Oliveira
Maths teacher
Would you like to reference this text in a school or academic work? Look:
OLIVEIRA, Raul Rodrigues de. "Angles on the circumference"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/angulos-no-circulo.htm. Accessed on June 27, 2021.


