When we study polyhedra, we come across the Plato's solids as a particular case. To be a Plato solid, the polyhedron must satisfy three conditions:
be convex;
all faces have the same amount of edges;
all vertices are ends of the same number of edges.
Several philosophers sought to understand the origin of the Universe, and Plato saw it in spatial geometry the explanation for this origin. Plato's solids are:
tetrahedron;
hexahedron;
octahedron;
dodecahedron;
icosahedron.
All of them are considered regular polygons, as their edges and their faces are all congruent. Plato's solids respect the Euler's relationship, which lists the number of vertices, faces and edges by the formula V + F = A + 2.
Read too: What are the differences between flat and spatial figures?

regular polyhedra
The search for regular polyhedra is recurrent, as they are easier to work with. A polyhedron is classified as regular if it has all the faces formed by the same polygon congruent. When this occurs, the angles and edges are also congruent.
Plato's solids are particular cases of regular polyhedra. The cube, for example, which is a Plato solid, has all of its faces formed by congruent squares. Of Plato's Five Solids, three are formed by triangular faces with congruent triangles, one is formed by square faces and the other is formed by pentagonal faces.
Do not stop now... There's more after the advertising ;)
What are Plato's solids?
Plato was a Greek philosopher and mathematician. He made great contributions to mathematics and, in trying to understand the Universe, associated solids with elements of nature.
To be a platonic solid, the polyhedron must be regular and convex. There are only five solids that satisfy this definition. They are: the tetrahedron, the cube or hexahedron, the octahedron, the icosahedron and the dodecahedron.
The relationship made between the element of nature and the solid was:
tetrahedron - fire
hexahedron - Earth
octahedron – air
icosahedron - Water
dodecahedron – Cosmo or Universe
To be a Plato solid, O polyhedron also needs to be convex, all faces must have the same number of edges and all vertices must be ends of the same number of edges.
See too: Cobblestones - geometric solids formed by flat and polygonal faces
regular tetrahedron
The regular tetrahedron is a polyhedron that has 4 faces, which justifies its name (tetra = four). all your faces are formed by triangles. It is shaped like a pyramid of triangular base and is known as a pyramid of regular base, since all of its faces are congruent. It has a total of 4 faces (in the format of equilateral triangle), 4 vertices and 6 edges.
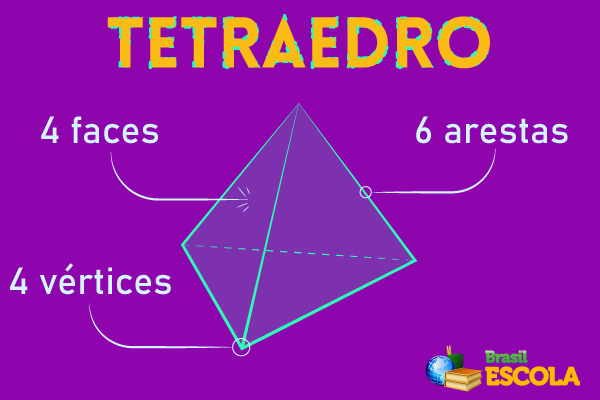
If you want to build your own regular tetrahedron, just download and print the PDF on here.
Regular cube or hexahedron
the regular hexahedron has 6 faces, which justifies its name (hex = six). your faces are all square. It is also known as a cube and has 6 faces, 12 edges and 8 vertices.
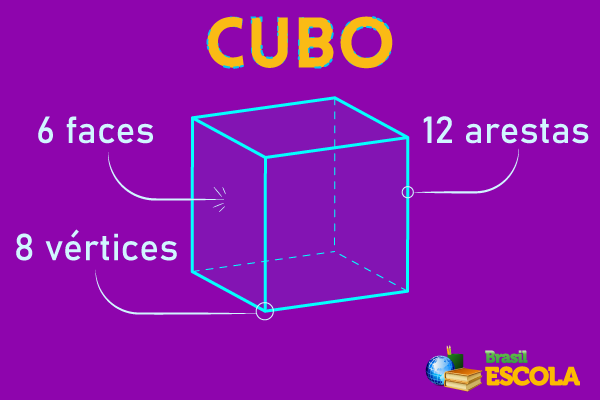
If you want to build your own cube, just download and print the PDF on here.
Octahedron
Like the previous ones, the name is linked to the number of faces, hence the octahedron has 8 faces. These faces have equilateral triangle shape. The octahedron has 8 faces, 12 edges and 6 vertices.

If you want to build your own octahedron, just download and print the PDF on here.
icosahedron
The icosahedron has a total of 20 faces. Their faces are shaped like equilateral triangles, just like the octahedron. It has a total of 20 faces, 30 edges and 12 vertices.

If you want to build your own icosahedron, just download and print the PDF on here.
Dodecahedron
The dodecahedron is the last of Plato's solids. It has a total of 12 faces and it is considered the more harmonic among the five Platonic solids. Their faces are shaped like pentagons. It features 12 faces, 30 edges and 20 vertices.
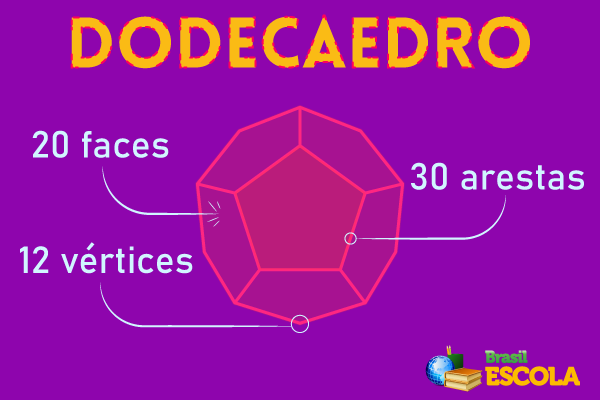
If you want to build your own dodecahedron, just download and print the PDF on here.
Also access: Cylinder - geometric solid formed by two parallel circular faces and in different planes
Euler's formula
Eulerian polyhedra are convex polyhedra. Euler developed a formula that relates the number of faces (F), number of vertices (V) and the number of edges (A) in a convex polyhedron. All Plato solids satisfy the Euler relation.
V + F = A + 2 |
Analyzing the formula, it is then possible to calculate the number of vertices from the number of faces and edges, or the number of faces from the number of vertices and edges, in short, knowing two of its elements, it is always possible to find the third.
Example:
Knowing that a polyhedron has 8 vertices and 12 edges and that it is regular, how many faces does it have?
We know that V + F = A+2
V = 8
A = 12
8 + F = 12 + 2
8 + F = 14
F = 14 - 8
F = 6
solved exercises
Question 1 - (Enem 2016) Plato's solids are convex polyhedra whose faces are all congruent to a single polygon regular, all vertices have the same number of incident edges and each edge is shared by only two. faces. They are important, for example, in classifying the shapes of mineral crystals and in the development of various objects. Like all convex polyhedrons, Plato's solids respect the Euler relation V - A + F = 2, where V, A and F are the number of vertices, edges and faces of the polyhedron, respectively.
In a crystal, whose shape is that of a triangular-faced Plato's polyhedron, what is the relationship between the number of vertices and the number of faces?
A) 2V - 4F = 4
B) 2V - 2F = 4
C) 2V - F = 4
D) 2V + F = 4
E) 2V + 5F = 4
Resolution
Alternative C. Since the faces are triangular, we know that for each face there are 3 edges. However, to relate the number of edges to the number of faces, it is important to remember that each edge is contained on two faces, because the meeting of two faces forms an edge, so we can relate edge to face in this case per:
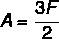
Having the Euler relation as V - A + F = 2 and substituting A, we have to:

Question 2 - From the alternatives below, judge which one is not a Plato solid.
A) Cube
B) Regular Tetrahedron
C) Icosahedron
D) Dodecahedron
E) Cone
Resolution:
Alternative E. Of the alternatives, the only one that does not correspond to a Plato solid is the cone.
By Raul Rodrigues de Oliveira
Maths teacher