We know that not all measurements we carry out give perfect results. The values we can find have limited accuracy by factors such as: the associated experimental uncertainty to any instrument, the skill of the experimenter and also the number of measurements carried out.
For example, if when we take a measurement of an object, we find the value of 3.7 cm, we will be presenting a two-digit result. These two digits are said significant algharisms, where the number 3 is the correct number; and 7 the dubious digit. At times we may come across significant figures with several decimal places. In these cases, we must be careful to perform some basic content, such as addition, subtraction, multiplication and division. Let's look at the correct procedures to perform such operations:
Addition and Subtraction
For addition or subtraction operations, we must first round the values of significant digits to leave them with the same number of decimal places. Below is a basic example for the sum of three length measurements made by different instruments: 47.186 m, 107.4 m and 68.93 m.
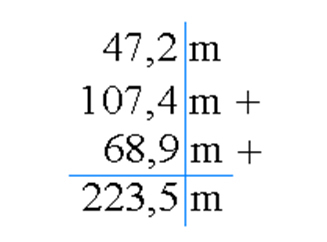
Thus, we can write the operation in the figure above as follows: S = 47.2 m + 107.4 m + 68.9 m, obtaining as a result S = 223.5 m. After the calculations, we chose as reference the number with the fewest decimal places. For subtraction operations we must follow the same reasoning as for addition, but following its certain rules.
Multiplication and Division
For multiplication and division operations, we perform the operations normally, and the final result should be written with the same number of significant digits as the factor with the least number of digits significant. Let's look at a basic example: calculating the measure of the area of the face of a door, which has a rectangular shape, measuring 2.083 m in length and 0.817 m in width:
The result obtained in the above multiplication must be rounded to have three significant figures, which correspond to the number of significant figures of the factor 0.817 m. Therefore, we must round the result, giving the answer 1.70 m2.
If an equation is being used, pure numbers cannot be taken into account as a reference for determining the significant figures. For example, the area of a triangle is given by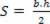 
, where b is the measure of the base and h is the height relative to that base. For a triangle with a base 2.36 cm and height 11.45 cm, the calculation of the area will be:
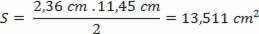
The result will be written S = 13.5 cm2 (so that it has only three significant digits, such as the 2.36 cm factor), since the number 2, in the denominator, did not serve as a parameter for determining the number of significant digits of the answer. It belongs to the equation, it is not the result of measurement.
By Domitiano Marques
Graduated in Physics
Source: Brazil School - https://brasilescola.uol.com.br/fisica/operacoes-com-algarismos-significativos.htm
