THE proportion is defined as the equality between two reasons, if this equality is true, then we say that the numbers that were the reasons in the given order are proportional.
The study of proportions is essential for mathematical development, as they enable us listgreatnesses, thus solving problems of our daily lives. Examples of proportions are: scale of a map, average speed of a rover, and density of a solution.
Read too: Problems involving fractional numbers
What is reason and proportion?
THE reason between two numbers is thequotientbetween them in the order in which they are given. Let a and b be two rational numbers, where b is different from 0, the ratio between a and b is given by:

when you have two reasons and both are being compared for an equality, then we have a proportion. If the equality is true then the numbers will be proportional, otherwise they will not be proportional.
You rational numbersThe, B, ç and d they are proportional if and only if the following equality is true.
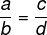
Similarly, we can say that the equality will be true only when the cross-multiplication is true.
a · d = b · c |
Do not stop now... There's more after the advertising ;)
Proportion Properties
Consider the following ratio between numbers The, B, ç and d:

So the following properties are valid:
Property 1 – The product of the means is equal to the product of the extremes (cross multiplication).
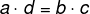
Property 2 – The reason between the sum (or difference) of the first two terms and the first term is equal to the ratio of the sum (or difference) of the last two terms and the third term.

Read too: Proportion properties – what are they and how to calculate?
How to calculate proportions
To check or calculate if, in fact, the numbers are proportional, just apply the first property, if the equality is true, then the numbers are proportional. See the examples:
Example 1
Check that the numbers 15, 30, 45 and 90 are proportional.
We must, in that order, assemble the ratios and then perform cross-multiplication.
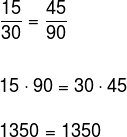
Note that the equality is true, so the numbers form, in that order, a proportion.
Example 2
The numbers 2, 4, x and 32 are known to be proportional. Determine the value of x.
By hypothesis, we have that the numbers, in the order they were presented, are proportional, so we can equalize the ratios between them and apply property 1, see:

Directly and inversely proportional quantities
Greatness, in math, it is everything that is possible to measure or measure, for example, quantity, distance, mass, volume etc. The quantities can be directly proportional (GDP) or inversely proportional (GIP), let's see the difference between them:
Directly proportional quantities
We say that two or more quantities are directly proportional if the ratio of values of the first quantity is equal to the values of the second quantity, and so on. For example, the mass quantity is proportional to the Weight of an object, see the table:
Mass (kg) |
Weight (N) |
30 |
300 |
60 |
600 |
80 |
800 |
Note that the ratio between the quantities is always the same:
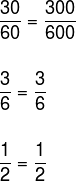
The same will happen if we realize the ratio between the other values.
Another way to know if two or more quantities are directly proportional is to check the growth or decrease of both. For example, if one quantity increases, the other must also increase if they are directly proportional. Let's look at the example:
In the mass x weight table, see that the greater the object's mass (↑), the greater its weight (↑), so the quantities are directly proportional.
Example
The numbers x, t and 2 are directly proportional to the numbers 5, 6 and 10. Determine the values of x and t.
As the example told us that the numbers are directly proportional, so the ratio between them is equal, like this:
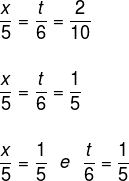
Multiplying each of the equalities, we have:
5x = 5
x = 1
and
5t = 6
t = 6 ÷ 5
t = 1.2
Therefore, x = 1 and t = 1.2.
Inversely proportional quantities
Two or more quantities will be inversely proportional if the ratio between the values of the first is equal to the inverse of the ratio of the values of the second. We can interpret it another way, if one quantity increases (↑) and the other quantity decreases (↓), then they are inversely proportional. See the example:
Speed and time are inversely proportional.
Speed (km/h) |
Time (hours) |
50 |
2 |
100 |
1 |
150 |
0 |
Note that the faster the speed of a given trip (↑), the shorter the time for that trip (↓). Also see that if we take the ratio between two values of the first quantity and the inverse of the ratio of two values of the second quantity, the equality will be true.
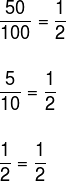
Example
Divide the number 120 into parts inversely proportional to the numbers 4 and 6.
Since we want to split the number 120 into two parts and we don't know them, let's call them The and 120 – a. By definition of inversely proportional, the ratio between the first values is equal to the inverse of the ratio of the last two values. Thus:
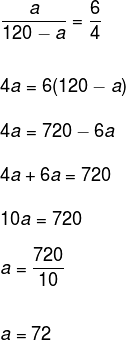
As the other part is 120 - a, then:
120 - the
120 – 72
48
Therefore, by dividing the number 120 into parts inversely proportional to the numbers 4 and 6, we get 72 and 48.

Exercise solved
Question 1 – (Fuvest) In the following table, y is inversely proportional to the square of x. Calculate the values of p and m.
x |
y |
1 |
2 |
2 |
0 |
m |
8 |
Resolution
Note that the statement states that the values of y are inversely proportional to the square of x, that is, the ratio of the y values will be equal to the inverse of the x squared values.

Using the same logic, let's determine the value of m.
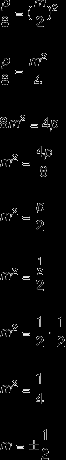
by Robson Luiz
Maths teacher