Diagonal on one polyhedron it is a straight segment that connects two of its vertices not belonging to the same face. Calculating the length of this diagonal is made by Pythagorean theorem. If this is done algebraically, the result is a formula able to perform this calculation.
You rectangular blocks they are straight prisms whose bases are rectangles. This type of prism has the following property: all sides of a straight prism are rectangles.
Rectangular block diagonal
To find the measurement of the diagonal of blockrectangular, use the following formula:

It is important to know the strategy used to find this formula, as it can also be used to find the diagonal of blockrectangular. This strategy is detailed below:
Finding the formula by Pythagoras' theorem
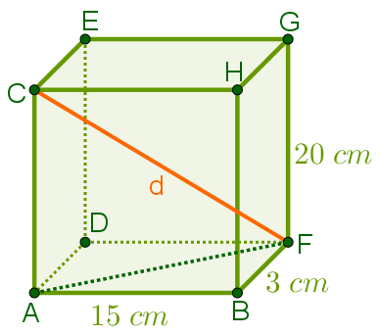
Consider that the following image is a blockrectangular, a is its length; b, its width; h, its height; and CF, one of your diagonals:
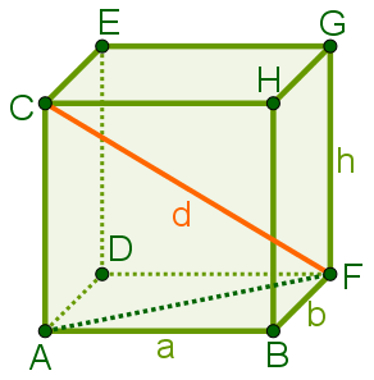
Note that ACF forms a right triangle. Also, notice that d (the diagonal measure of the blockrectangular) is also the hypotenuse of this triangle, so it can be obtained by
theorem in Pythagoras. However, it is necessary to know the measure of the AF segment.To find this measurement, notice that ABF is also a right triangle, and the hypotenuse is precisely the AF segment. We can also calculate it using Pythagoras' theorem, since we know the measures a and b of their legs.
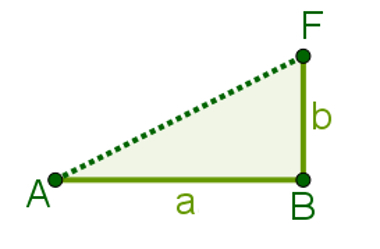
Fur theorem in Pythagoras:
Do not stop now... There's more after the advertising ;)
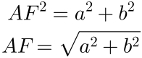
From the length of AF, we can find the length of d, which is the diagonal of blockrectangular. To do this, look again at the right triangle ACF:

Put the AF segment measurement as done in the image above and use the theorem in Pythagoras to find the measure of segment d:
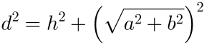
Once that's done, use the properties of the radicals to find:

In this way, if necessary, use the theorem in Pythagoras to find the measurement AF of the right triangle; then use the same theorem to find the measure of the diagonal of blockrectangular.
Example
One blockrectangular it is 15 cm long, 3 cm wide and 20 cm high. Calculate the measure of diagonal of this polyhedron and then use Pythagoras' theorem to confirm your result.
Solution
With the formula, we will find the diagonal of that blockrectangular in the following way:
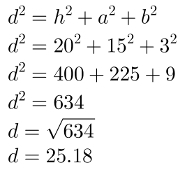
THE diagonal measures approximately 25.18 cm.
By Pythagoras' theorem, we have:
Let's calculate the AF measure with the theorem in Pythagoras:
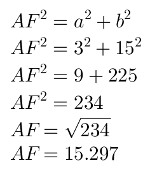
From the length of the AF segment, we can calculate the diagonal of blockrectangular:
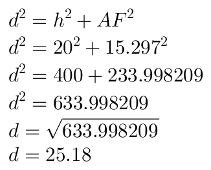
THE diagonal measures approximately 25.18 cm.
By Luiz Paulo Moreira
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Luiz Paulo Moreira. "Diagonal of rectangular block"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/diagonal-bloco-retangular.htm. Accessed on June 27, 2021.