As we studied statics, we saw that this is the branch of physics that is concerned with investigating the conditions under which a body is in equilibrium. Because they are different situations, we study separately the equilibrium conditions for bodies that can be treated as material points and for bodies that cannot be considered as such - in this case called bodies hard. Our object of study in this article is related to extended body balance.
We can then say that a body is considered rigid when the positions of the particles that make up the body do not change position during the time it is studied. Let us then consider that a rigid body is subject to the action of forces on the same plane. Thus, we say that this body is in balance when it is at the same time in balance of rotation and translation.
In order to guarantee the balance of the rigid extended body subject to a system of forces, we must impose some simultaneous conditions. Let's see below what these conditions are:
THE first
condition is that the resultant force systems must be null, that is, the resultant force acting on the rigid body system must be equal to zero, so we have:
translation balance
The second condition is that the algebraic sum of the moments of the forces of the system, with respect to an arbitrary pole, must be null. That is:
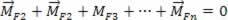
rotation balance
By Domitiano Marques
Graduated in Physics
Source: Brazil School - https://brasilescola.uol.com.br/fisica/equilibrio-corpo-extenso.htm
