O circle is flat geometric figure defined as the region bounded by a circle. THE circumference, in turn, is a set of points equidistant from another point called the center. The distance between the center of a circle and any point belonging to it, therefore, it is always the same and it's called lightning.

From this definition, and using analytic geometry, it is possible to find the reduced equation of the circumference.
(x – a) ² + (y – b) ² = R²
This equation involves a point P(x, y) on the circle, center C(a, b) and radius (R).

The figure above shows that it is possible to draw infinite circles using just 2 points, so you need to know the location of at least three points, whether they all belong to the circumference or just two that belong to it plus the center.
To find the center of a circle, just know the location of three points belonging to it.. For example:
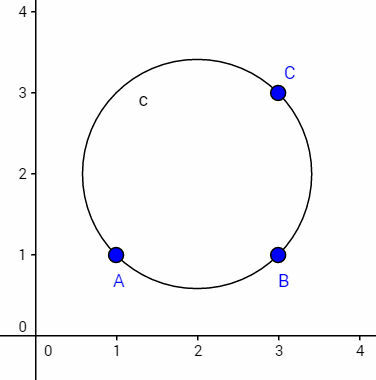
The highlighted points on the circle are A(1,1); B(3.1) and C(3.3) and its radius measures 1.41 cm. To find the center D(x, y), it is necessary to assemble the system of equations:
I) (1 - x) ² + (1 - y) ² = 1.41²
II) (3 - x) ² + (1 - y) ² = 1.41²
Do not stop now... There's more after the advertising ;)
III) (3 - x) ² + (3 - y) ² = 1.41²
By developing the first and second equations of the system above, we will have:
I) 1 - 2x + x² + 1 - 2y + y² = 1.41²
II) 9 - 6x + x² + 1 - 2y + y² = 1.41²
Decreasing equation I by equation II, we obtain:
8 - 4x = 0
8 = 4x
x = 8
4
x = 2
If equations II and III are developed, the results will be:
II) 9 - 6x + x² + 1 - 2y + y² = 1.41²
III) 9 - 6x + x² + 9 - 6y + y² = 1.41²
Decreasing III by II:
8 - 4y = 0
8 = 4y
y = 8
4
y = 2
Therefore, the ordered pair where the center of this circle is located is D(2,2)
In short: To find the center of a circle, just choose three known points belonging to it, replace their coordinates in the equation reduced from the circle so that the first point forms an equation, the second point forms a second equation, and the third point a third equation. After that, consider these three equations as a system and solve it. This procedure is suitable for finding the center of a circle.
By Luiz Paulo Moreira
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Luiz Paulo Moreira. "How to find the center of a circle"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/como-encontrar-centro-uma-circunferencia.htm. Accessed on June 28, 2021.