THE ball is a geometric solid studied in spatial geometry, being classified as a round body. This shape is quite common in everyday life, as we can see it on soccer balls, pearls, the globe, some fruits, among other examples.
considering O the origin and r the radius, the sphere is the set of points that are at a distance equal to or less than the distance between the radius and the origin. In addition to the radius, the sphere has important elements, like the poles, the equator, the meridian and the parallels. We can also divide the sphere into parts like the stamp and the spherical spindle. The total area and volume of a sphere are calculated by specific formulas that depend only on the radius value of that figure.
Read too: Differences between flat and spatial figures

Elements of a sphere
We know as a sphere all points in space that are within a distance equal to or less than the radius of its origin, so two important elements of this figure are the radius r and the origin O. The sphere is classified as a
round body due to the shape of its surface.
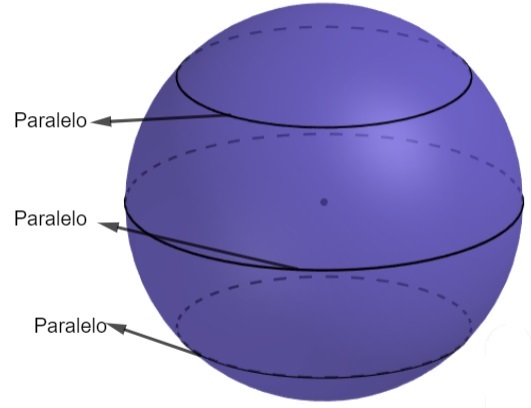
Other important elements for the sphere are the poles, equator, parallels and meridian.
- poles: represented by points P1 and P2, are the meeting points of the sphere with the central axis.

- Ecuador: the largest circumference we get by intercepting the sphere by a horizontal plane. The equator divides the sphere into two equal parts known as hemispheres.

- Parallels: any circumference that we achieve by intercepting the sphere by a horizontal plane. The equator, which we showed earlier, is a particular case of parallels and the largest of them.
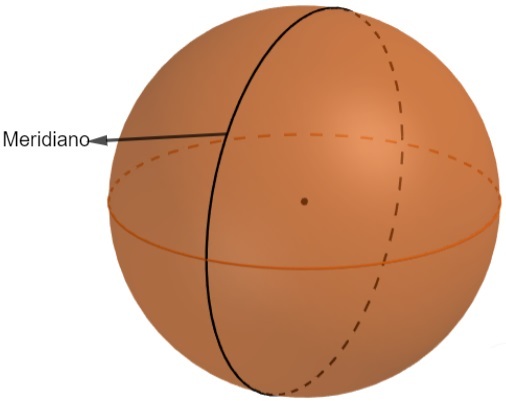
- Meridian: the difference between meridian and parallels is that the first is obtained vertically, but it is also a circumference contained in the sphere and obtained by intercepting a flat.
Learn more about the elements of this important geometric solid by reading: ANDelements of a sphere.
Sphere Volume
Calculating the volume of geometric solidss is of great importance for us to know the capacity of these solids, and with the sphere it is no different, it is of great importance to calculate its volume for know, for example, the amount of gas we can put in a spherical container, among others applications. The volume of a sphere is given by the formula:

Example:
A gas reservoir has a radius equal to 2 meters, knowing this, what is its volume? (use π = 3.1)

surface of the sphere
We know as the surface of the sphere the region formed by all points that are at a distance r from the sphere. Note that in this case the distance cannot be smaller, but exactly equal to r. The surface of the sphere is the contour of all solid, it is the surface that covers the sphere. To calculate the surface area of the sphere, we use the formula:
| THEt = 4 π r² |
Example:
In a hospital, an oxygen gas reservoir will be built in the shape of a sphere. Knowing that it has a radius of 1.5 meters, what will its surface area be in m²?
THEt = 4 π r²
THEt = 4 π 1,5²
THEt = 4 π 2,25
THEt = 9 π m²
See too: Wedis the difference between circle and circumference?
parts of the sphere
We can divide the sphere into parts, known as a spindle, when considering only its surface, or as a wedge, when considering the solid.
spherical spindle
The spindle is the surface formed by the rotation of a semicircumference when this rotation (θ) is less than 360º, that is, when 0 < θ < 360º.
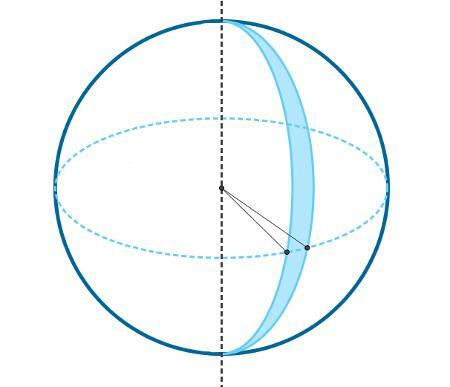
As the spindle is part of the surface of a sphere, we calculate its area, which can be deduced by a rule of three, generating the following formula:

Example:
Calculate the spindle area and wedge volume knowing that θ = 30º and r = 3 meters.

spherical wedge
We call spherical wedge the geometric solid formed by the rotation of a semicircle, when this rotation is less than 360º, that is, 0 < θ < 360º.
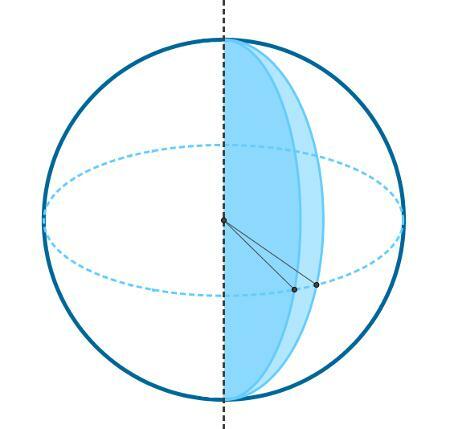
As the wedge is a geometric solid, we calculate its volume, which, as well as the spindle area, can be done through a rule of three, which generates the formula:
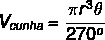
Example:
Calculate the wedge volume knowing that r = 4 cm and θ = 90º:

solved exercises
Question 1 - When analyzing a virus under a microscope, it was possible to see that it has two layers, being the first layer formed by fat and the central layer formed by genetic material, as shown in the image. follow:

One of the interests of this researcher is to know the volume of the fat layer of this virus. Knowing that the largest radius measures 2 nm (nanometers) and that the smallest radius measures 1 nm, the volume of the fat layer is equal to:
(use π = 3)
a) 4 nm³
b) 8 nm³
c) 20 nm³
d) 28 nm³
e) 32 nm³
Resolution
Alternative D.
Calculating the volume of the blue layer, that is, of fat, is the same as calculating the difference between the volume of the larger sphere VAND and the smaller sphere Vand.
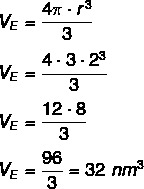
Now we will calculate the volume of the smaller sphere:
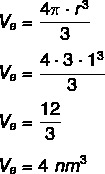
So the difference between the volumes is equal to:
VE - Ve = 32 - 4 = 28 nm³
Question 2 - A factory produces storage compartments, in the shape of a sphere, using a special plastic. Knowing that the cm² of this material costs R$ 0.07, the amount spent to produce 1,200 object holders, whose radius is 5 cm, will be:
(use π = 3.14)
a) BRL 2180
b) BRL 3140
c) BRL 11,314
d) BRL 13,188
e) BRL 26,376
Resolution
Alternative E.
Let's calculate the total area of a sphere:
At = 4 π r²
At = 4 · 3.14 · 5²
At = 12.56 · 25
At = 12.56 · 25
At = 314 cm²
By multiplying 314 by 0.07, we will have the value of a storage compartment, so if we multiply this value by 1.2 thousand, we will have the total amount spent.
V = 314 · 0.07 · 1200 = 26,376
By Raul Rodrigues de Oliveira
Maths teacher

