Area calculation is an everyday activity in all of our lives. We always find ourselves involved in some situation where there is a need to calculate the area of a flat geometric shape. Whether in the acquisition of land, in the renovation of a property or in the search to reduce packaging costs, the use of knowledge in calculating areas is present. It's a very simple activity, but sometimes we let some issues go unnoticed.
A math teacher, during the plane geometry class, asked his students the following question: We have a rectangle with an area of x square meters. If we double the measurements of the sides of this rectangle, what happens to the area value? One of the students immediately replied: the area will double in size, that is, it will be 2x square meters! The teacher immediately replied: By no means will it be more than double.
Let's see the explanation of this fact.
First, we'll make an example knowing the measurements of the rectangle, then we'll make the generalization.
Example 1. Consider the rectangle below:
Your area will be:
THE1 = 10 x 3 = 30 cm2
Now, let's double the side measurements.
The area of this new rectangle will be:
THE2 = 20 x 6 = 120 cm2
Note that by doubling the measurements of the sides of the rectangle its area more than doubled, actually quadrupled. But does this happen for any rectangle?
Now let's look at a generic case in order to check this property for every rectangle.
Let's consider a rectangle of base b and height h, as shown in the figure.
Your area is given by: A1 = a x h
Now, let's double your measurements, so the base will be 2b and the height will be 2h.
The area of this rectangle will be given by: A2 = 2b x 2h = 4(b x h) = 4A1.
Note that for any rectangle, if we double the measurements of its sides, the area will quadruple.
Let's analyze this situation for other flat figures.
Circumference:
On a circle of radius r, the area will be: πr2.
If we double the radius measure, that is, the radius being 2r, the area will be: π(2r)2 = π4r2 = 4πr2.
We can see that by doubling the radius value, the area of the circle also quadruples.
Do not stop now... There's more after the advertising ;)
Equilateral triangle
In an equilateral triangle of side L, its area will be:
When we double the measure on the side, that is, the triangle has a side measuring 2L, the area will be: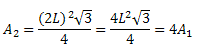
We conclude that by doubling the measurements of the sides of an equilateral triangle, its area quadruples.
In general, the conclusion is that, when doubling the measure of the dimensions of a flat figure, its areas have the value more than doubled.
By Marcelo Rigonatto
Specialist in Statistics and Mathematical Modeling
Brazil School Team
plane geometry - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
RIGONATTO, Marcelo. "Analysis of the polygon area"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/analise-area-dos-poligonos.htm. Accessed on June 28, 2021.