Resistor association: what is it, types, formulas

Associationinresistors is the electrical circuit formed by two or more elements of electrical resistance ohmic (constant), on in series, parallel or still, in a mixed association. When connected in series, the resistors are traversed by the same electric current, when in parallel, the electric potential it is the same for the associated resistors.

Lookalso: Ohm's First Law: Calculating Electrical Resistance

Resistors

Resistors are elements whose main purpose is to generation of heat through the passage of electric current. Electrical resistance, in turn, concerns the characteristic of resistors, which makes them offer load handling resistance inside.

In the figure, we have a ceramic resistor, present in most electrical circuits.

When a resistor has a constant electrical resistance, for any value of electrical potential that is applied between its terminals, we say that it is a ohmic resistor. To learn more about these elements, read: resistors.

equivalent strength

Equivalent resistance is a resource used to

simplify electric circuits formed by resistor associations, or even to obtain electrical resistances different from those we have. When we calculate the equivalent resistance we try to find what is the resistance of a single resistor that equals the resistance of the set of resistors.

• Association of series resistors

When connected in series, the resistors are traversed by the same electric current. In series connection, all connected elements are connected on the same branch of the circuit, so that the terminal of one of the resistors is directly connected to the terminal of the next resistor. The following figure shows how a serial connection is made and how this connection is represented:

In series connection, the electrical current is the same for all resistors.

When the resistors are connected in series, the potential that is applied across the circuit terminals is distributed between the resistors, in other words, all the applied voltage gradually drops along a circuit that is made up of series resistors.

In this type of call, the individual electrical resistances add up, so that the equivalent resistance of the circuit is given by the sum of the resistances connected in series. Watch:

In series connection, the equivalent resistance is equal to the sum of the resistances.

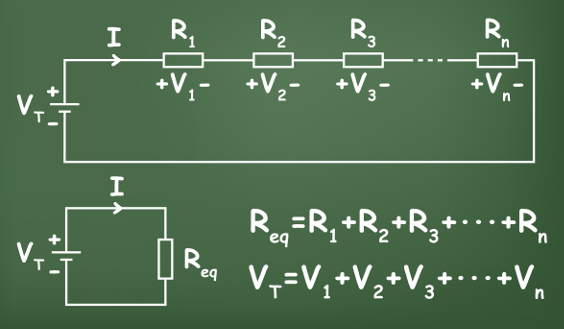
In short:

• In series connection, the resistances are added,
• In series connection, the electrical potentials add up,
• In series connection, the electrical current is the same for all resistors.

Below, we show the formula used to calculate the equivalent resistance for series resistors:

R_EQ – equivalent resistance (Ω – ohm)

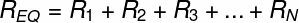
• parallel association

In parallel association, the resistors are connected to the same electrical potential, however, the electrical current passing through each resistor can be different if the resistors have different electrical resistances.

In parallel association, the electrical current is divided between the different branches of the circuit.

Parallel association is obtained when the resistors are connected so that the electric current splits as it passes through them. In this type of association, the equivalent electrical resistance will always be smaller than the smallest resistance.

To calculate the equivalent resistance in the association of resistors in parallel, we add the inverse of the individual resistances:

For the case where you want to calculate the resistance of only two resistors in parallel, it is possible to do this through the product of the sum of the individual resistances. Check out:

Another specific case is the one in which N identical resistors are connected in parallel. In this case, to calculate the equivalent resistance of the circuit, just divide the individual resistance value by the number of resistors:

In short:

• In parallel connection, the electrical current is divided according to the electrical resistance of each branch;
• In parallel connection, the equivalent resistance is less than the smallest resistance;
• In parallel connection, all resistors are connected under the same electrical potential.

• Mixed association of resistors

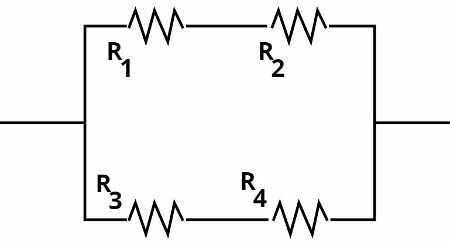
In the mixed association of resistors, there may be so muchConnectionsinserieshow muchConnectionsinparallel. See the figure below, you can see several resistors connected in series, connected to two resistors that are connected in parallel to each other:

To solve it, it is necessary to solve separately, the resistors that are connected in parallel and the resistors that are connected in series.

• When there are series resistors outside the parallel connection, it is possible to resolve the association in parallel to then add the result obtained to the resistance of the other resistors connected in series;

Subtitle

• When there are resistors connected in series within a parallel connection, it is necessary to add the resistances so that we can then perform the calculation of the equivalent resistance in parallel.

In this type of association, initially, R is added₁ and R₂, then R₃ and R_4.

Lookalso:Electric generators: what they are and how to calculate electromotive force

solved exercises

Question 1) Four ohmic resistors with resistances equal to 10 Ω, 20 Ω, 30 Ω and 40 Ω are connected in series and then in parallel. The values ​​obtained for the equivalent resistance in each of these cases are, respectively, equal to:

a) 150 Ω and 36 Ω

b) 10 Ω and 92 Ω

c) 100 Ω and 4.8 Ω

d) 15 Ω and 12 Ω

e) 30 Ω and 90 Ω

Resolution

Alternative c. To calculate the equivalent resistance in series, it is enough to add each one of the resistances, in this way, the equivalent resistance of the association in series will be 100 Ω. In order for us to calculate the equivalent resistance of this set of resistors, when associated in parallel, we must do the following calculation, note:

To perform the calculation presented, it was necessary to calculate the least common multiple between the numerators 10, 20, 30 and 40. We then cross-multiply, resulting in an equivalent resistance less than the smallest of the resistances and equal to approximately 4.8 Ω.

Question 2) Calculate the approximate equivalent resistance of a mixed association where two resistors, 10 Ω and 20 Ω, are associated in series with two other resistors, 30 Ω and 40 Ω, associated in parallel.

a) 80Ω

b) 47 Ω

c) 33 Ω

d) 51 Ω

e) 27 Ω

Resolution:

Alternative b. First, we add the resistances of 10 Ω and 20 Ω, resulting in 30 Ω. Then we make the product by adding the resistances of 30 Ω and 40 Ω, resulting in 120/7 Ω, approximately 17.1 Ω. The sum of these equivalent resistances is therefore approximately 47 Ω.

By Rafael Hellerbrock
Physics teacher

Source: Brazil School - https://brasilescola.uol.com.br/fisica/associacao-resistores.htm