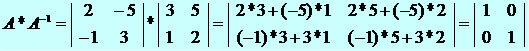To understand what a complementary event is, let's imagine the following situation:
When rolling a dice we know that the sample space is composed of 6 events. Starting from this release, we will only consider events with face values less than 5, given by 1, 2, 3, 4, totaling 4 events. In this situation we have that the complementary event is given by numbers 5 and 6.
The union of the event in question with the complementary event forms the sampling space and the intersection of the two events forms an empty set. See an example based on these conditions:
Example 1
In the simultaneous roll of two dice, let's determine the probability of not rolling a 4.
In the roll of two dice we have the sample space of 36 elements. Considering the events where the sum is four, we have: {(1, 3), (3, 1), (2, 2)}. Probability of exiting adds four equals: 3 out of 36, which corresponds to 3/36 = 1/12. To determine the probability of not leaving, add four, we perform the following calculation:
Do not stop now... There's more after the advertising ;)

In the expression, we have that the value 1 refers to the sample space (100%). We have that the probability of not coming out adds up to four when rolling two dice is 11/12.
Example 2
On the roll of a perfect die, what is the probability that the number 6 will not come out.
Probability of not getting the number 6 = 1/6

The probability of not coming out the 6 is 5/6.
by Mark Noah
Graduated in Mathematics
Brazil School Team
Probability - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Probability of a Complementary Event"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/probabilidade-um-evento-complementar.htm. Accessed on June 28, 2021.