To determine the inverse matrix of a square matrix A of order n, it is enough to find a matrix B such that the multiplication between them results in an identity matrix of order n.
A*B = B*A = Ino
We say that B is the inverse of A and is represented by A-1.
Remember that the identity matrix of order n (In) is a matrix where the elements of its main diagonal are equal to 1 and the other elements are equal to 0. For example: 
Example 1
Given matrices A and B, check if one is the inverse of the other. 
Multiply the matrices and verify that the result consists of an identity matrix. 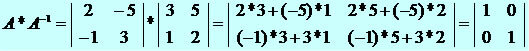
Do not stop now... There's more after the advertising ;)
We can verify that A-1 it is the inverse of A, since the multiplication between them resulted in an identity matrix.
Example 2
Let's determine if the inverse matrix of A exists. 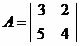
To determine the inverse of a matrix, simply multiply the matrix given by a generic matrix of terms a11, b12, c21, d22, given the equality of an identity matrix. Watch:
Solving systems: 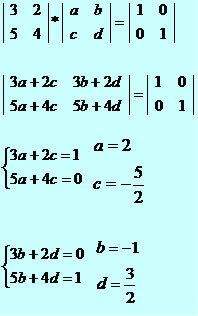
So, we have that the inverse matrix is: 
by Mark Noah
Graduated in Mathematics
Brazil School Team
Matrix and determinants - Math - Brazil School
Would you like to reference this text in a school or academic work? Look:
SILVA, Marcos Noé Pedro da. "Existence of an inverse matrix"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/existencia-uma-matriz-inversa.htm. Accessed on June 28, 2021.


