O Venn diagram, also known as a Venn-Euler diagram, is a way to graph a set, for this we use a closed line that does not have self-intersection and we represent the elements of the set inside this line. The idea of the diagram is to facilitate understanding in the basic set operations, such as: inclusion and belonging relationship, union and intersection, difference and complementary set.
Read too: Operations between integers: know the properties
Venn diagram representations
As shown, the Venn diagram consists of a closed (non-intertwining) line on which we “place” the elements of the set in question, so we can represent one or several sets simultaneously. See the examples:
• Single set
We can represent you using a single closed line, for example, let's represent the set A = {1, 3, 5, 7, 9}:
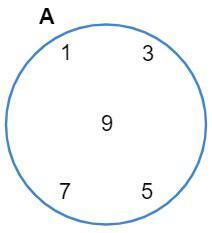
• Between two sets
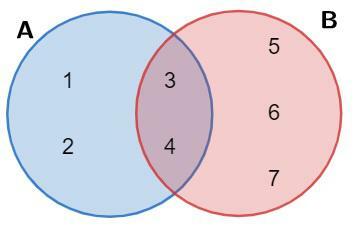
We must make two graphs like the one representing the single set. However, from operations with sets we know that: given two sets, they may or may not intersect. If the two sets do not intersect, they are named disjoint sets.
Example 1
Plot, using the Venn diagram, the sets A = {a, b, c, d, e, f} and B = {d, e f, g, h, i}.
Note that the intersection is the part of the diagram that belongs to the two sets, just like in the definition.
A ∩ B = {d, e, f}

Example 2
Plot the sets C = {a, b, c, d} and D = {e, f, g, h}.
Note that the intersection of these sets is empty, as it does not have any element that belongs simultaneously to both, that is:
C ∩ D = { }

• Between three sets
The idea behind the representation using the Venn diagram for three sets is similar to the representation between two sets. In this sense, sets can be disjoint one by one, that is, they do not have any intersection; or they can be disjoint two by two, that is, only two of them intersect; or all intersect.
Example
Representation, using the Venn diagram, of sets A = {a, b, c, d}, B = {d, e, f, g} and C = {d, e, c, h}.
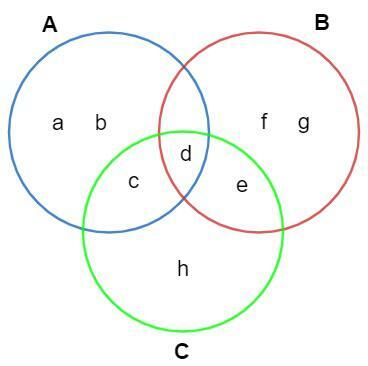
See too: Important set notations
Do not stop now... There's more after the advertising ;)
membership relationship
The membership relationship allows us to say whether an element belongs or not to a certain set. For this, we use the symbols:

Consider the set A = {a, b, c, d}. Analyzing it, we realize that g, for example, does not belong to him, so in the Venn diagram, we have:
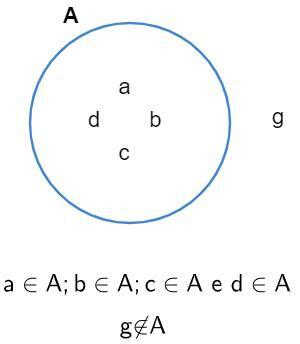
Inclusion relationship
The inclusion relationship allows us to say whether or not a set is contained in another set. When a set is contained in another, we say that it is a subset. For this we use the symbols:

An example of this is the relationship between the set of natural numbers and set of whole numbers. We know that the set of natural numbers is a subset of the set of integers, that is, the set of naturals is contained in the set of integers.
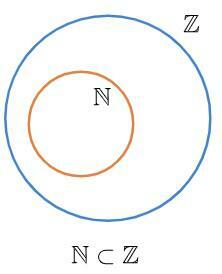
Operations between sets
The basic operations between two or more sets are: unity, intersection and difference between two sets.
• Union
The union between two sets is formed by joining the elements contained in each set, in other words: all elements of the two sets are considered. Look:
Consider the sets A = {1, 2, 3, 4} and B = {3, 4, 5, 6, 7}. The union between them is given by:
A U B = {1, 2, 3, 4, 5, 6, 7}
In the Venn diagram, we shaded the union part, that is, both sets, check:
• Intersection
The intersection is a new numerical set formed by elements that belong, simultaneously, to other sets. Generally speaking, the intersection between sets in the Venn diagram is given by the part common to the graphs involved. Look:
Considering again the sets A = {1, 2, 3, 4} and B = {3, 4, 5, 6, 7}, we have that the elements that belong to the set A and to the set B, simultaneously, are:
A ∩ B = {3,4}
• Difference between two sets
Consider two sets C and D, the difference between them (C – D) will be a new set formed by elements belonging to C and not belonging to D. In general, we can represent this difference, using the Venn diagram, as follows:

solved exercises
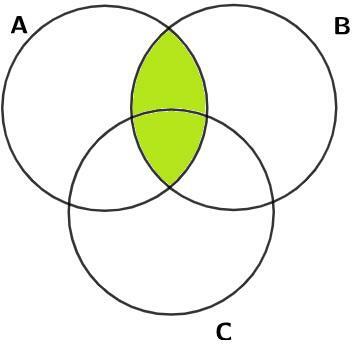
question 1 – (Ufal) In the following figure, non-disjoint sets A, B and C have been represented. The colored region represents the set:

a) C – (A ∩ B)
b) (A ∩ B) – C
c) (A U B) - C
d) A U B U C
e) A ∩ B ∩ C
Solution
Alternative b.
Remembering the operations with sets, we know that the intersection between two sets in the Venn diagram is given by the part common to them. Considering sets A, B and C and coloring the set intersection A ∩ B, we have:
Title: Solution question1 – part 1
Note that if we remove the elements from the set C, we get the colored part requested by the exercise, that is, we must initially highlight the intersection and then remove the elements from C.
(A ∩ B) – C

question 2 – (Uerj) Children at a school participated in a vaccination campaign against infantile paralysis and measles. After the campaign, it was found that 80% of children received the paralysis vaccine, 90% received the measles vaccine, and 5% received neither.
Determine the percentage of children at this school who received both vaccines.
Solution
As the percentage of children who received both vaccines is unknown, let's initially call it x. Remember that we must not operate with the % symbol, but write the exercise percentages in their decimal or fractional form.
80 % → 0,8
90% → 0,9
5% → 0,05
100% → 1
To find out the total number of children who took only the paralysis vaccine, we subtracted the verified percentage (80%) of the percentage of those who took both (x), and the same should be done for children who only took the vaccine against the measles. Thus:

Joining all the children, the percentage will be 100%, therefore:
0.9 - x + x + 0.8 - x + 0.05 = 1
1.75 - x = 1
– x = 1 – 1.75
(–1) · – x = – 0.75 · (–1)
x = 0.75
x = 75%
Therefore, 75% of the children at the school had both vaccines.
By L.do Robson Luiz
Maths teacher

