Energyinternal is the sum of kinetic energies and potential related to the movement of the constituent atoms and molecules of a body. The internal energy is also directly proportional to the temperature of the body. It is a scalar quantity measured in Joules (SI) and determined as a function of variables such as pressure (P), volume (V) and temperature thermodynamics (T) of a system, in Kelvin (K).
The higher the temperature of a body, the greater its internal energy, therefore, the greater its ability to do some work. Furthermore, the internal energy of monoatomic gases, for example, is given exclusively by the sum of the kinetic energy of every atom of the gas. When dealing with molecular gases, such as diatomic gases, one must take into account molecular interactions and, for this, the internal energy is determined by the sum of the kinetic energy of the molecules with the potential energy existing between they.
Do not stop now... There's more after the advertising ;)
Internal energy of ideal monoatomic gases
As there is no interaction between the atoms of an ideal monoatomic gas, its internal energy depends exclusively on two variables: the number of moles (n) and the gas temperature (T). Watch:
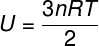
U – internal energy
no – number of moles
R – universal constant of perfect gases
T – temperature
In the equation above, R it has a modulus of 0.082 atm. L/mol. K or 8.31 J/mol. K (SI). Also, we can write the above equation in terms of other quantities, such as pressure and volume. For that, we need to remember the Clapeyron's Equation, used for ideal gases.
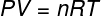
Substituting the above equation for the previous one, we will have the following expression for the calculation of the internal energy:
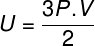
Lookalso:What is a perfect gas?
Taking the above equations into account, it is possible to determine a relationship between the kinetic energy of the atoms of an ideal monoatomic gas and its temperature. For this, we will state that the kinetic energy of this type of gas is purelykinetics. Watch:
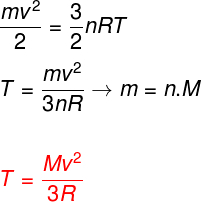
m - pasta
no – mole number
M - molar mass
In many situations, it is interesting to know how to calculate the variation of the internal energy (ΔU) of a gas, as this quantity indicates whether the gas has received or gave in energy. If the variation of the internal energy of the gas has been positive (ΔU > 0), the gas will have received energy; otherwise (ΔU< 0), the gas will have given up part of its energy.
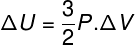
Internal energy variation in terms of gas volume variation.
Internal energy for diatomic gases
For ideal diatomic gases, the internal energy is given by a slightly different equation.
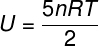
Internal energy in thermodynamic transformations and cycles
According to the 1st Law of Thermodynamics, the internal energy of an ideal gas may vary in certain thermodynamic transformations, depending on the amount of heat exchanged between the surroundings and the system, as well as the work performed by or on the system.
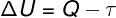
Q – heat
τ - work
Next, let's look at the form this law takes for some particular thermodynamic transformations.
Lookalso:History of thermal machines
→ Internal energy: isothermal transformation
At isothermal transformation, there is no temperature change and therefore the internal energy remains constant.
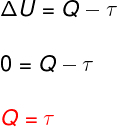
In this case, the entire amount of heat that is exchanged with the system is turned into work and vice versa.
→ Internal energy: isovolumetric transformation
At isovolumetric transformation, it is not possible to carry out work, since the system is confined in a rigid and inexpandable container. In this case, the entire amount of heat that is exchanged with the system directly varies its internal energy.
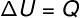
→ Internal energy: isobaric transformation
In this type of transformation, the system is subjected to a constant pressure, therefore, the work done by him or on him can be calculated analytically.
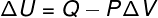
→ Internal energy: adiabatic transformation
In the adiabatic transformations, there is no heat exchange between the system and its surroundings, therefore, the variation of the internal energy depends exclusively on the work performed by or on the system.
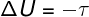
Internal energy in cyclic processes
In every cyclic process, the thermodynamic state of a system, represented by its pressure, volume and temperature variables (P, V, T), is transformed, but ends up returning to the original state (P, V, T), therefore, the variation of internal energy in this type of process is always null (ΔU = 0).
Lookalso:Cyclic transformations
Look at the graph below, which shows three distinct thermodynamic transformations between states A and B.

As the three transformations (I, II and III) leave state A and go to state B, the internal energy variation must be equal for all of them, therefore:

Internal energy exercises
1) Two moles of an ideal diatomic gas, with a molar mass equal to 24 g/mol, are found at a temperature of 500 K inside a closed, rigid container with a volume equal to 10-3 m³. Determine:
a) The modulus of the internal energy of this gas in joules.
b) The pressure that the gas exerts on the walls of the container.
Resolution:
The) Since it is an ideal and diatomic gas, we will use the formula below to calculate its internal energy:
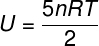
Taking the data that were informed in the exercise statement, we will have the following calculation to be solved:
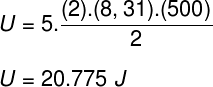
B) We can determine the pressure that the gas exerts once we know the volume of its container: 10-3 m³. To do this, we will use the following formula:
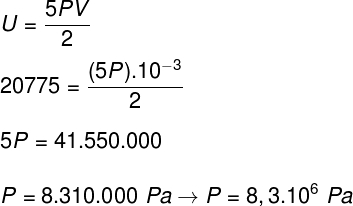
By Me. Rafael Helerbrock