O dot product between two vectors is a real number that relates the magnitude of these vectors, that is, their length, and the angle between them. To calculate it, it is therefore necessary to know their lengths and the angle they form.
Using the plane as a basis, a vector indicates a location, intensity, direction and direction. Therefore, it is used in the studies of Mechanics (Physics) as a representative of a force applied to an object.
The usual representation of the vector is an arrow that ends at a point. The coordinates of this point are said to be the coordinates of the vector starting from point O (0,0). We write v = (a, b) to represent it. Thus, the vector v = (1,2) is drawn as follows:
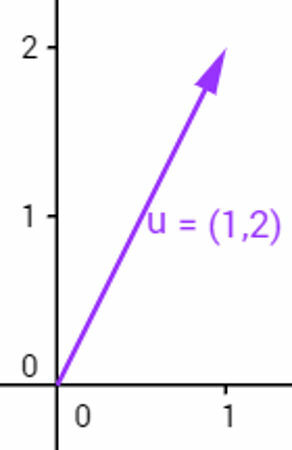
Vector example starting from the origin
To calculate the length of this vector, consider the right triangle formed by it and its projection on the x-axis (or y-axis), as shown in the following figure:
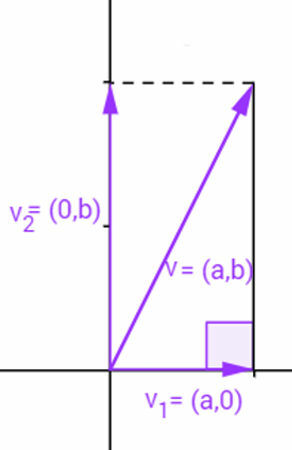
Length of vector v
The length of a vector v is called v vector norm or vector module v and is represented by |v|. Note that the norm of the vector v = (a, b) is precisely the measure of the hypotenuse of the triangle represented in the figure above. To calculate this measure, we use the Pythagorean Theorem:
|v|2 = the2 + b2
|v| = √(a2 + b2 )
Two vector dot product
Given two vectors u and v, the inner product between them is represented by and is defined as:
= |u||v|·cosθ
This is a kind of multiplication between two vectors, however, it is not called a product as it is not a common multiplication, since it involves the angle formed by these two vectors.
Angle between two vectors
The first result arising from the above definition is the angle between two vectors. With the real numbers “dot product”, “u vector norm” and “v vector norm”, it is possible to calculate the angle between vectors u and v. To do this, just perform the calculations:
Do not stop now... There's more after the advertising ;)
= |u||v|·cosθ
= cosθ
|u||v|
Therefore, dividing the inner product by the norms of the vectors u and v, we find the real number referring to the cosine between these two vectors and, therefore, the angle between them.
Note that if the angle between two vectors is straight, cosθ is equal to zero. Therefore, the above product will have the following result:
= 0
From this, it can be concluded that, given two vectors u and v, they will be orthogonal if = 0.
Inner product calculated from vector coordinates
Considering the two vectors u = (a, b) and v = (c, d), the dot product between u and v is given by:
= = a·c + b·d
Internal product properties
Given the vectors u, v and w and the real number α, note:
i) =
This means that the inner product of vectors is “commutative”.
ii) = +
This property is comparable to the distributivity of multiplication over addition.
iii) = = α
Calculating the inner product between u and v multiplied by the real number α is the same as calculating the inner product between αv and u or between v and αu.
iv)
The inner product of v with v is only zero if v is the null vector.
v)
The inner product of v with v will always be greater than or equal to zero.
By Luiz Paulo Moreira
Graduated in Mathematics