Trigonometry is a word of Greek origin that refers to the measure of three angles. Studies in this area of Mathematics focus on triangles, which are polygons that have three sides and, consequently, three angles. At first, the trigonometry it is concerned with studying some properties and relationships of right triangles to later relate the measurements of the sides of the triangles with the measurements of the angles.
These properties and relationships are expanded to any triangles through theorems known as sins law and cosine law. Later, some of these results are observed in triangles whose sides are notable segments of a circle, which is known as a “trigonometric circle”.
THE trigonometry proposes a great novelty. Before it, it was only possible to consider calculations and properties involving exclusively sides or exclusively angles of a triangle or basic relationships between these elements. Upon its arrival, it is possible to directly relate the measurements of the sides of a triangle to the measurement of one of its angles. It is noteworthy that the relationships between the notable sides and segments within a triangle also make up the
trigonometry.Before delving into the concept of trigonometry, It is important to know what are the most important elements in a right triangle. These elements are set out below:
Elements of a right triangle
Every right triangle can be subdivided into two other right triangles, as shown in the figure below, tracing the height “h” relative to the base “a”.
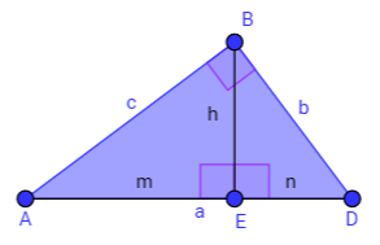
The height of this right triangle forms two 90° angles with its base
Considering triangle ABD, rectangle in B, it is possible to observe the following elements:
1 – The sides AB and BD are called sides and their measurements are c and b, respectively;
2 – The AD side is called the hypotenuse and its measurement is a. This side will always be opposite the 90° angle;
3 – BE is the height of triangle ABD relative to base AD and its measurement is h. (remembering that the height always forms an angle of 90° with the base relative to it);
4 – AE is the orthogonal projection of the AB leg over the hypotenuse. Its measure is m;
5 – ED is the orthogonal projection of the BD leg over the hypotenuse. Its measurement is n.
Next, we present and discuss some properties seen in trigonometry, based on the elements of the right triangle exposed above.
Metric Relations in the Right Triangle
They are equalities that relate sides, height and orthogonal projections of a right triangle:
1) c2 = average
2) b·c = a·h
3) h2 =m·n
4) b2 = no
5) the2 = b2 + c2 (Pythagorean theorem)
Trigonometric ratios or ratios in the right triangle
These equalities relate ratios between the sides of a right triangle to one of its acute angles. To do so, it is necessary to fix one of the two angles and observe, in the right triangle, the definitions of opposite side and adjacent side:

Rectangle triangle, highlighting the α angle
BD is the opposite leg to angle α;
AB is the adjacent leg to angle α.
Do not stop now... There's more after the advertising ;)
These are the prerequisites for defining the trigonometric ratios. Are they:
→ Sine of α
sin α = Cathetus opposite α
Hypotenuse
→ Cosine of α
cos α = Catheto adjacent to α
Hypotenuse
→ Tangent of α
tg α = Cathetus opposite α
Catheto adjacent to α
These reasons apply to any right triangle that has an acute angle equal to α. The result of these divisions is always the same, regardless of the length of the side of the triangle, as two triangles that have two equal angles, due to the triangle likeness angle-angle, have proportional sides. Hence it follows that the ratio between the sides is equal.
trigonometric circle
Also called a trigonometric cycle or trigonometric circle (more correct but less common names), it is an oriented circle of radius 1. On this circumference, a right triangle, whose angle α coincides with the origin, so that the height of this triangle goes from the abscissa axis to the edge of the circle.
This height coincides with the value of sine, because it is the opposite side to angle α. The measure that goes from the point where the height meets the axis of the abscissa to the origin coincides with the side adjacent to angle α, that is, with the value of cosine.
These coincidences occur because the hypotenuse is always 1, as it is the radius of the circle. Note these properties in the image below:
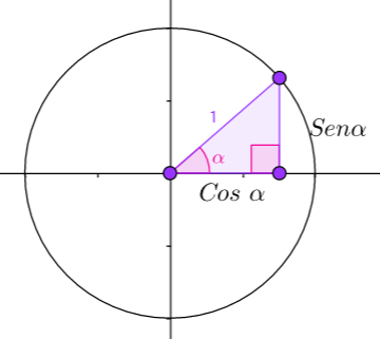
Circle of radius 1, on which a right triangle is placed to evaluate its properties
Whatever the right triangle constructed on that circle, the side that coincides with a part of the abscissa axis measures exactly the cosine value of α and the other side measures exactly sine of α.
Trigonometric Functions
Using the trigonometric circle, it is possible to define trigonometric functions that relate each element of the set of real numbers to a single element also of the set of real numbers. However, these numbers are expressed in radians, which is a unit of measure as a function of π used because, after 360° in the trigonometric circle, the counting of degrees and, consequently, of the domain and counter-domain elements of a function based on it can be restarted from zero.
fundamental relationships
The fundamental relationships of trigonometry are:
1) Fundamental relationship 1
Sen2α + cos2α = 1
2) tangent of α
tg α = sin α
cos α
3) Cotangent of α, which is the inverse of the tangent of α
cotg α = cos α
sin α
4) Secant of α, which is the inverse of the cosine of α
sec α = 1
cos α
5) Cossecant of α, which is the inverse of the sine of α
cossec α = 1
sin α
6) Relation arising 1
tg2α + 1 = sec2α
7) Relation 2
cotg2α + 1 = cossec2α
8) Recurring relationship 3
cotg α = 1
tg α
By Luiz Paulo Moreira
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Luiz Paulo Moreira. "What is trigonometry?"; Brazil School. Available in: https://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-trigonometria.htm. Accessed on June 27, 2021.
function, trigonometric function, tangent, cosine, sine, cosecant, cotangent, arc, angles, value of the arc, trigonometric function value, relationship between angle and trigonometric function, relations derivatives.
radian, angle, degree, circle, arc, arc of circle, transformation from degree to radian, Definition of radian, angle measure, arc measure, circumference length in radian, length of circumference.