Two competing straight lines make four angles. Analyzed in pairs, it is possible to notice that these angles are either side by side or only have a single point in common, which is also the meeting point of the two straight lines. When two angles have this last characteristic, they are called angles opposite by vertex.
The other two angles, which are side by side, are called adjacent angles.
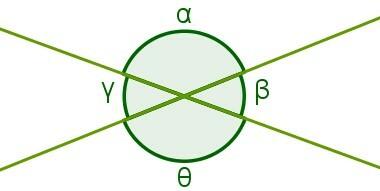
Angles opposite by vertex and adjacent angles on concurrent lines
properties
adjacent angles are supplementary;
anglesoppositesfurvertex they are congruent, that is, they have equal measures. Note the following angles:

If α, β and θ are the measures of angles in question, the sums α + β and β + θ are equal to 180° because the respective angles they are adjacent. So we can write:
α + β = 180 and β + θ = 180
From the two equalities above, we can write the following:
180 = 180
α + β = β + θ
Do not stop now... There's more after the advertising ;)
α = β – β + θ
α = θ
Soon, the anglesoppositesfurvertex are congruent.
Examples
1º) What is the measure of angle α in the following figure?
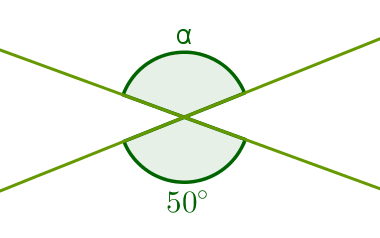
Solution:
Note that the angle of 50° is apex opposite angle α, so α = 50°.
2º) Calculate the measurement of each angle in the figure below.

Solution:
Knowing that anglesoppositesfurvertex are congruent, just observe the following equation:
10x + 50 = 4x + 110
10x - 4x = 110 - 50
6x = 60
x = 60
6
x = 10
To find out the measure of each angle, just substitute the value of x in one of the expressions:
10x + 50 =
10·10 + 50 =
100 + 50 =
150°
Like the angles they are oppositesfurvertex, the other angle also measures 150°.
By Luiz Paulo Moreira
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Luiz Paulo Moreira. "What are angles opposed by the vertex?"; Brazil School. Available in: https://brasilescola.uol.com.br/o-que-e/matematica/o-que-sao-angulos-opostos-pelo-vertice.htm. Accessed on June 27, 2021.