irrational equations have the unknown located in the radical, that is, inside the root. Thus, to solve an irrational equation, it is necessary to keep in mind the root properties.
Generally speaking, for this resolution, we use the equivalence principle to "get out" of the irrational case and arrive at a equation of the first or high school.
Read too: Differences between function and equation
How to solve an irrational equation
To solve an irrational equation, we must use the equivalence principle in order to “eliminate” the radicals, that is, we must raise both sides of the equation to the root index, since, when this property is used, the stem “disappears”. Look:
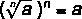
Once this procedure is performed, the equation is no longer irrational and becomes rational, and thus, to solve it, we use the already known methods. See the following example:
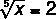
Note that the index of the radical is the number 5, so to solve this equation, we must raise both sides to the fifth power. Look:
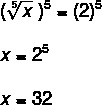
Therefore, the solution set is given by:
S = {32}
Do not stop now... There's more after the advertising ;)
Of course there are more complex cases, but the method of solving will always be the same. Look at one more example:

Note that to solve such an irrational equation, we must find a way to eliminate the radical which has index 2, that is, we must square both sides of the equation and then solve the equation, check:
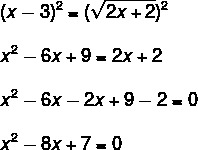
Note that from an irrational equation we fall into a quadratic equation, and now it is enough to solve it using the method of bhaskara.
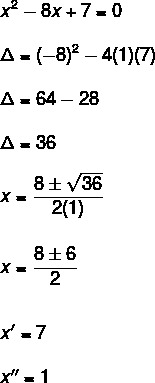
Therefore, the solution set is given by:
S = {7, 1}

See too: Radical reduction at the same rate
solved exercises
question 1 – (PUC-Rio) The number of solutions of the equation, with x > 0, is equal to:

a) 0
b) 1
c) 2
d) 3
e) 4
Solution
Alternative b. To solve the following equation, we must square its sides, since the exponent index is equal to 2.
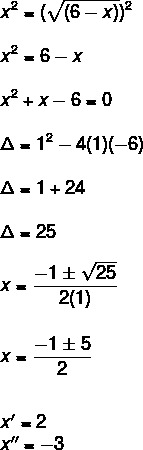
Note that the statement asks us the number of solutions greater than zero, so we have a solution greater than zero.
question 2 – (UTF-PR) Adriana and Gustavo are participating in a competition in the city of Curitiba and received the following task: bring the picture of the building located at Rua XV de Novembro, number N, such that a and b are the roots of the equation irrational.

Solution
For Adriana and Gustavo to be able to take the photograph, they must determine the building number, that is, the number N. For this, we determine the numbers a and b, which are solutions to the irrational equation.
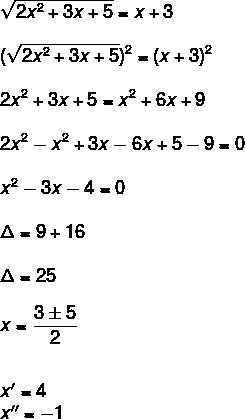
According to the statement, the values of a and b are the respective roots of the irrational equation, so we have to:
a = 4 and b = – 1
Now, to find out the value of N, just replace the values of a and b in the given expression.
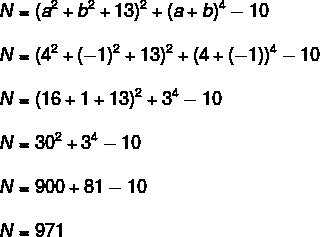
Therefore, the building number is 971.
by Robson Luiz
Maths teacher
Would you like to reference this text in a school or academic work? Look:
LUIZ, Robson. "Irrational Equations"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/equacoes-irracionais.htm. Accessed on June 28, 2021.