THE first degree equation with an unknown is a tool that solves big problems in math and even in our daily lives. These equations come from polynomials grade 1, and its solution is a value that resets such a polynomial, that is, finding the unknown value and substituting it in the expression, we will find a mathematical identity that consists of a true equality, for example, 4 = 22.
What is a 1st degree equation?
One equation of first degree is a expression where the degree of the unknown is 1, that is, the exponent of the unknown is equal to 1. We can represent an equation of the first degree, in general, as follows:
ax + b = 0
In the case above,x is the unknown, that is, the value we should find, and The and B are called coefficients of the equation. the coefficient value The must always be different from 0.
Read too: Mathematical Problems with Equations
Examples of 1st Degree Equations
Here are some examples of first degree equations with an unknown:
a) 3x +3 = 0
b) 3x = x (7+3x)
c) 3 (x –1) = 8x +4
d) 0.5x + 9 = √81
Note that, in all examples, the power of the unknown x is equal to 1 (when there is no number in the base of a power, it means that the exponent is one, that is, x = x1).
Do not stop now... There's more after the advertising ;)
Solution of a 1st degree equation
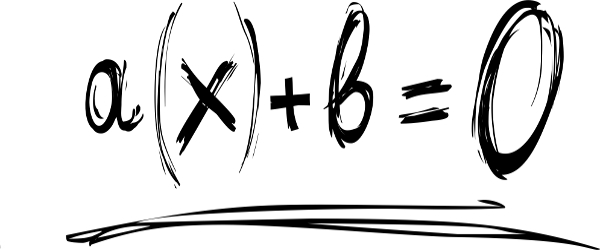
In an equation, we have an equality, which separates the equation into two members. Of left side of equality, let's have the firstmember, It's from sideright, O second member.
ax + b = 0
(1st member) = (2nd member)
To keep equality always true, we must operate on both the first and second member, or that is, if we perform an operation on the first member, we must perform the same operation on the second. member. This idea is called principle of equivalence.
15 = 15
15 + 3= 15 + 3
18 = 18
18– 30= 18 – 30
– 12 = – 12
Note that the equality remains true as long as we operate simultaneously on both members of the equation.
The equivalence principle is used to determine the unknown value of the equation, that is, to determine the root or solution of the equation. To find the value of x,we must use the equivalence principle to isolate the unknown value.
See an example:
2x – 8 = 3x – 10
The first step is to make the number – 8 disappear from the first member. For this, let'sadd the number 8on both sides of the equation.
2x - 8+ 8= 3x - 10+ 8
2x = 3x - 2
The next step is to make 3x disappear from the second member. For this, let'ssubtract 3x andm both sides.
2x– 3x =3x – 2– 3x
– x = – 2
Since we're looking for x, not –x, let's now multiply both sides by (–1).
(– 1)· (–x) = (–2) · (– 1)
x = 2
The solution set of the equation is therefore S = {2}.
Read too: Differences between function and equation
Mallet for First Degree Equation Solution
There is a trick arising from the equivalence principle that makes it easier to find the solution to an equation. According to this technique, we must leave everything that depends on the unknown in the first member and everything that does not depend on the unknown in the second member. To do this, just "pass" the number to the other side of the equality, changing its sign for the opposite sign. If a number is positive, for example, when passed to the other member, it will become negative. If the number is multiplying, just “pass it” by dividing and so on.
Look:
2x – 8 = 3x – 10
In this equation, we have to "pass" the–8for the second member and the3xto the first, changing their signals. Thus:
2x– 3x = –10+ 8
(–1)· – x = –2 ·(– 1)
x = 2
S = {2}.
Example
Find the solution set of equation 4 (6x – 4) = 5 (4x – 1).
Resolution:
The first step is to carry out the distributivity, then:
24x – 16 = 20x – 5
Now, organizing the equation with the values that accompany the unknown on one side and the others on the other, we will have:
24x - 20x = –5 + 16
4x = 11
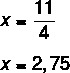
Read too:Fractional Equation – How to Solve?
solved exercises
question 1 – Double a number added with 5 equals 155. Determine this number.
Solution:
Since we don't know the number, let's call it n. We know that double any number is twice itself, hence double no is 2n.
2n + 5 = 155
2n = 155 - 5
2n = 150
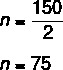
Reply: 75.
question 2 – Roberta is four years older than Barbara. The sum of their ages is 44. Determine the age of Roberta and Barbara.
Solution:
As we don't know the age of Roberta and Barbara, let's name them as r and B respectively. As Roberta is four years older than Barbara, we have to:
r = b + 4
We also know that the sum of the ages of the two is 44 years old, so:
r + b = 44
Replacing the value of r in the equation above, we have:
r + b = 44
b + 4 + b = 44
b + b = 44 - 4
2b = 40

Reply: Barbara is 20 years old. As Roberta is 4 years older then she is 24 years old.
by Robson Luiz
Maths teacher