trigonometric ratio – also called trigonometric relation – is, roughly speaking, the result of dividing the measurements of two sides of a right triangle. Trigonometric ratios are able to relate the sides to the angles of a right triangle. If it weren't for them, it would only be possible to build what we know as metric relationships.
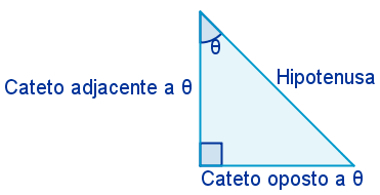
Before defining the trigonometric ratios, it is important to know the nomenclature of the sides of a right triangle.
rectangle triangle
In any right-angled triangle, the side opposite the right angle – which is the longest side of the triangle – is called hypotenuse. The other two are named after peccaries.
Furthermore, by setting the acute angle θ of any right-angled triangle, the side opposite this angle is called opposite leg, and the side that touches this angle is called theadjacent leg.
Trigonometric ratios
The trigonometric ratios were created from the following observation: Two right triangles that have a second congruent angle are similar. This means that between these two triangles, the side measurements are proportional and the angle measurements are congruent. In this way, taking an acute angle from a right triangle, the ratio between its sides will have the same result.
This information is important for trigonometry because a trigonometric ratio related to a given angle will have a fixed value for any triangle, regardless of the size of its sides, because since they are proportional, the ratio of the corresponding sides will be equal.
That said, we will define the trigonometric ratios sine, cosine and tangent:
Senθ = Cathetus opposite θ
Hypotenuse
Cosθ = Cathetus adjacent to θ
Hypotenuse
Tgθ = Cathetus opposite θ
Cathetus adjacent to θ
A value for each angle
The sine of an angle is invariant regardless of the measure of the side of the triangle from which that angle was taken. The following triangle was constructed in the computer, so that it had a right angle and a 30º angle, represented by the Greek letter θ. The measurements obtained were:
Do not stop now... There's more after the advertising ;)

Calculating the sine of 30°, we will have:
Sen30 = Cathetus opposite θ = 2,31 = 0,5
Hypotenuse 4.62
The value 0.5 is the 30° sine for any triangle. This is because all triangles that have two congruent angles are proportional. In this example, 0.5 is just the ratio found in right triangles that have an angle of 30°.
trigonometric table
The above calculations can be done for all “whole” angles - an angle can also be fractionated. “Decimal” fractions are called minutes and “centesimals” are called seconds. Using the sine, cosine and tangent ratios, it would be possible to build the following table of values:

practical applications
Through trigonometric reasons, it is possible to relate the angles of a right triangle with the values of its sides. Therefore, it is possible to find the measure of one side of a right triangle by having only the measures of one of its acute angles and one of its sides. Look at the example:
Calculate the value of the length side The in the following triangle:

In this triangle, we want to find the value of the side opposite the 60° angle from the value of its adjacent side. watching the trigonometric ratios defined above, we observe that the only one that relates the opposite side to the adjacent side is the tangent. Therefore, we will use this reason to find the value of “a”. Looking for the 60° tangent in the table above, we find the value: 1.732. Look at the calculations used to find the measure on side a:
Tg60 = Cateto opposite 60 = The
Cathetus adjacent to 60 2
Tg60 = The
2
1,732 = The
2
a = 1.732·2
a = 3.464
By Luiz Paulo Moreira
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Luiz Paulo Moreira. "What is trigonometric ratio?"; Brazil School. Available in: https://brasilescola.uol.com.br/o-que-e/matematica/o-que-e-razao-trigonometrica.htm. Accessed on June 27, 2021.