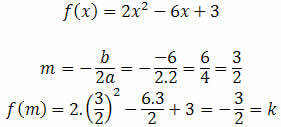The study of progressions is based on sequences that have a mathematical pattern. According to this pattern, it is possible to determine several elements of a sequence just by knowing its first element and the reason for that sequence.
In certain situations it is necessary to calculate the sum of terms in a given sequence. In the sequences of the geometric progression type, we can find two types of summation, the summation of finite terms and the summation of infinite terms - Sum of Terms of an Infinite PG. We will then see the expression to calculate the sum of finite terms of a P.G, using only the term a1 and the ratio q.
Therefore, let us see the demonstration of the Sum expression of P.G. finite.
Be the1, a2, …, Theno) a P.G, in which its ratio is: q ≠ 1
Therefore, the expression that represents the sum of these n terms is given as follows:
Do not stop now... There's more after the advertising ;)
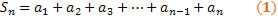
Let's do a multiplication by q in the entire expression, that is, we must multiply both sides of the equality:

Let's subtract expression (2) by expression (1):
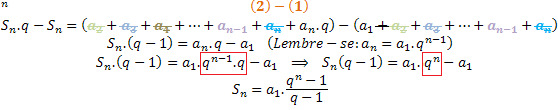
Note that to use this expression, we must have a ratio other than 1.
It is noteworthy that we could have subtracted expression 1 from expression 2. If we do this, we will get the following expression:
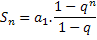
With this we just learn to use these expressions (which are the same, it's up to you to decide which one to use) to solve issues involving this concept.
By Gabriel Alessandro de Oliveira
Graduated in Mathematics
Brazil School Team
Would you like to reference this text in a school or academic work? Look:
OLIVEIRA, Gabriel Alessandro de. "Sum of a finite P.G."; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/soma-uma-pg-finita.htm. Accessed on June 28, 2021.