Let's imagine that we witness a head-on collision between a wall and a popular car that moves with a small speed. In this collision, we saw that the car recoiled a little at the time of the crash. But if instead of a car it were a bus, with the same speed, we would probably witness the destruction of the wall and we would also see that the bus would continue advancing moments after the collision.
Returning to the initial situation, if the car is moving at a relatively high speed and collides with the wall, we can say that its movement after the collision will be a little different than that of the situation previous. The car can then destroy the wall; and also, after the collision, it can continue its movement. Thus, we can conclude that for a certain mass, the amount of movement is greater for higher speeds.
We associate an orientation to the description of the movements that appear coupled. For example, a swimmer pushes water back and advances forward. In this case, we are saying that the swimmer's speed has one direction and one direction while the speed of the pushed portion of water has the same direction but opposite direction.
In the examples mentioned above, we look for clues that allow us to state that the amount of movement of the systems remains constant, during the time the interaction occurred, that is, from the instant immediately before to the instant immediately after the collision.
Most collisions, however, are not head-on. In a game of pool, for example, one ball might collide with another ball slightly sideways or graze, and the two move away in different directions. However, even in these situations, the amount of movement of the system is conserved.
Generally speaking, the conservation of momentum in the system is one of the fundamental principles of physics, used to calculate the recoil velocity of weapons, to design space rockets, industrial machines, etc.
Let's consider a mass body m which, at a given moment, has speed v in relation to a given referential. we name amount of movement or linear momentum of this body the vector quantity given by the product of the mass (m) of the body by its speed (v), in the adopted framework. Mathematically, we define the movement quantity Q with the product
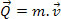
Thus, we can conclude that the value of Q has the following characteristics:
- direction: coincident with the direction of velocity v
- sense: equal to velocity v (because m is positive)
- module: Q = m.v
- SI unit: [Q] = kg.m.s-1
By Domitiano Marques
Graduated in Physics
Source: Brazil School - https://brasilescola.uol.com.br/fisica/uma-grandeza-vetorial-que-se-conserva.htm

