One occupation is a rule that relates each element of a set A, called domain, to a single element of a set B, called a counter-domain. Also, in functions, the subset of the counterdomain that has all elements related to at least one element of the domain is called a Image.
Functions can be classified as injectors, surjective or bijectors, according to how the elements of the domain interact with the elements of counter-domain. In this article, we discuss the concept and characteristics of functions. surjective.
Concept of surjective function
A role is considered surjective when all the elements of your counter-domain are related to at least one element of the domain. This definition is equivalent to saying that the counterdomain of a surjector function is equal to its image, because, in this type of function, every element of the counterdomain is an image of some element of the domain.
The following diagram shows an example of a function whose counterdomain is the same as the image:
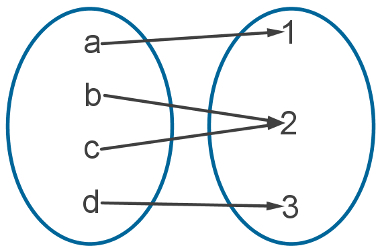
Note that this
occupation é surjective and that there are no “remains” elements in their counter-domain, and this is another characteristic of the surjective functions.Surjective function: formal definition
Consider the occupation f, with domain in set to and with counter-domain in set B, defined as f(x) = y. The function f is surjective if, and only if, for every y belonging to the counterdomain B, there is an x belonging to the set A, such that f(x) = y. Algebraically, we have:
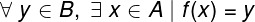
This symbology can be “translated” as: “for every y belonging to B, there is x belonging to A, such that f(x) = y”.
The other way to define a occupationsurjective is, given the function f of domain A and counterdomain B:
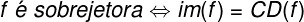
Examples
The function f(x) = x, with domain and counter-domain reals, is surjective because every value of y belonging to the counterdomain is equal to x belonging to the domain.
The function f(x) = x2, with domain and counter-domainreal, it is not surjective, because y belonging to the counterdomain is positive, however, there are negative values in this set. Therefore, the counterdomain and the image of this function are different.
The function f(x) = x2, with domain and counter-domain equal to the set of non-negative reals, it is surjective, since the counterdomain only has positive numbers and zero and, thus, the counterdomain and the image are the same set.
By Luiz Paulo Moreira
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/o-que-e/matematica/o-que-funcao-sobrejetora.htm

