Given any circle with center O and radius r, we mark two points A and B, which divide the circle into two parts called arc of circumference. Points A and B are the extremes of the arcs. If the ends are coincident, we have an arc with a complete loop. Note the following illustration:

We can note in this circle the existence of the arc AB and a central angle represented by α. For each arc existing in the circle, we have a corresponding central angle, that is: avg (AÔB) = avg (AB). Therefore, the length of an arc depends on the value of the angle central.
At measuring arcs and angles, we use two units: the degree it's the radian.
Measures in degree
We know that a complete turn around the circumference corresponds to 360°. If we divide it into 360 arcs, we have unit arcs measuring 1 degree. In this way, we emphasize that the circumference is simply a 360° arc with the central angle measuring one complete revolution, or 360°. We can also divide the 1-degree arc into 60 arcs of unit measures equal to 1’ (one-minute arc). Likewise, we can divide the 1’ arc into 60 arcs of unit measures equal to 1” (arc of one second).
Measurements in radians
Given a circle with center O and radius R, with an arc of length s and α the central angle of the arc, let's determine the measure of the arc in radians according to the following figure:
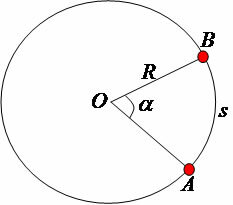
We say that the arc measures one radian if the length of the arc is equal to the measure of the radius of the circumference. So, in order to know the measure of an arc in radians, we must calculate how many radii of the circle are needed to get the length of the arc. Therefore:
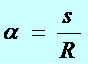
Based on this formula we can express another expression to determine the length of an arc of a circle:
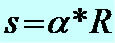
According to the relationships between the degree and radian measurements of arcs, we will highlight a rule of three capable of converting the measurements of arcs. Look:
360º → 2π radians (approximately 6.28)
180º → π radian (approximately 3.14)
90° → π/2 radian (approximately 1.57)
45º → π/4 radian (approximately 0.785)
measure in |
measure in |
x |
α |
180 |
π |
Examples of conversions:
a) 270º in radians
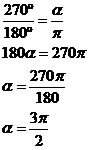
b) 5π/12 in degrees
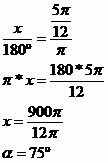
by Mark Noah
Graduated in Mathematics
Brazil School Team
Trigonometry - Math -Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/medida-de-um-arco.htm


