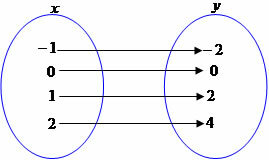
Every function is defined by a formation law, this is how we relate two sets A and B. Functions are used to express situations based on algebra, generalizing problems through formulas. For example, the function y = 2x or
f (x) = 2x shows that y values depend on x values. In this case we have that y corresponds to the double of x. See the relationship between some of the x and y values:
f: R→R such that f (x) = 2x
Example 2
The function that represents the square of a number is given by the function f (x) = x² or y = x². It is considered a function that has domain and image in reals.
f: R→R such that f (x) = x² 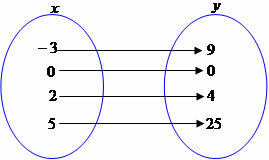
Example 3
The following function represents the successor of the double of a number and is given by the following expression: y = 2x + 1 or f (x) = 2x + 1. 
Example 4
The function f(x) = x² + x is considered a function of the 2nd degree. In this case it represents the square of a number added to the number itself. In this way we can build the following diagram:

Example 5
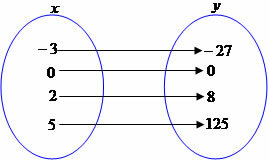
The function f(x) = x³ is a function with characteristics to represent the cube of any rational number.
by Mark Noah
Graduated in Mathematics
Brazil School Team
Roles - Math - Brazil School
Source: Brazil School - https://brasilescola.uol.com.br/matematica/funcao-definida-por-formula.htm
