Powers are the result of products where all factors are equal. They are uniquely represented through a base, which is the number multiplied, and of a exponent, which is the amount of times that number is multiplied. When the exponent of a power is negative, we need to use some of the potency properties to be able to calculate it. One of these properties is the potency of fractions, and the other is the potency itself with negative exponent.
Powers with negative exponent
when a potency It has exponentnegative, the property used to calculate it is as follows:
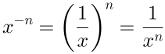
That property is usually read as follows: when a power has a negative exponent, invert its base and also the sign of exponent. So to resolve potencies whose exponent é negative, proceed as follows:
write to base gives potency in the form of a fraction;
reverse the base and also the sign of exponent;
-
Make the calculations and, if necessary, with the potency properties.
Do not stop now... There's more after the advertising ;)
power of fractions
They are potencies whose base it's a fraction. To solve them, just raise the numerator and denominator separately to the exponent of that power. Watch:
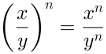
At the power above, we calculate xno and yno to get the result.
1st Example - Calculate the following negative exponent power:
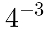
Solution: first, we wrote to base gives potency in fraction form. Then we apply the power property with exponentnegative and finally we solve each power separately. Watch:
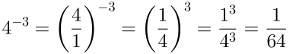
2nd Example - Calculate the following negative exponent power:
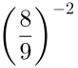
Solution: do exactly the same as in the previous example. The only difference is that it is not necessary to write the base in fraction form, as it is already like this.

By Luiz Paulo Moreira
Graduated in Mathematics
Would you like to reference this text in a school or academic work? Look:
SILVA, Luiz Paulo Moreira. "Power with negative exponent"; Brazil School. Available in: https://brasilescola.uol.com.br/matematica/potencia-com-expoente-negativo.htm. Accessed on June 28, 2021.



