We can define a spherical lens as being an association of two flat diopters, one of which is necessarily spherical, while the other can be spherical or flat. Therefore, here we will treat as a spherical lens any transparent body bounded by two surfaces of a diopter.
As for the nomenclature of spherical lenses, we have:
- thin edge lenses: biconvex, plano-convex and concave-convex
- thick edge lenses: biconcave, plano-concave and convex-concave.
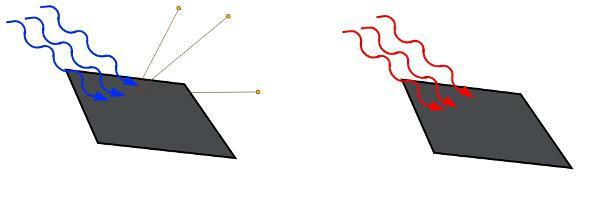
Through an analytical study we can determine the height and position of an image conjugated by a spherical lens. For this, it is enough that we know the position and size of the object. Let's see the figure below:
Let's suppose we have an object MN placed in front of a converging spherical lens. The image produced by this lens is defined by making use of only three light rays that come out of the object. We can see, in the figure above, that the formation of the image takes place exactly at the point of intersection between the light rays.
Do not stop now... There's more after the advertising ;)
In the figure above we have the figure of two triangles (painted part). Taking as mathematical bases the similarity of triangles in the figure above, we can relate the abscissa Pand P', of the object and the image, with focal length fof the lens.
Therefore, we have:
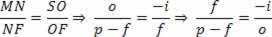
But, by the linear increase equation,


p.p'-p'.f = p.f
p.p' = p'.f+p.f
Multiplying the two members of the last expression by

We get:
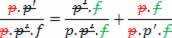
Which results in:

The above expression is known as the conjugate points equation or Gauss equation.
By Domitiano Marques
Graduated in Physics
Would you like to reference this text in a school or academic work? Look:
SILVA, Domitiano Correa Marques da. "Equation of Conjugated Points"; Brazil School. Available in: https://brasilescola.uol.com.br/fisica/equacao-dos-pontos-conjugados.htm. Accessed on June 27, 2021.