O It is madephotoelectric is a physical phenomenon that consists of the emission of electrons by certain materials, usually metallic, when illuminated by electromagnetic waves of specific frequencies. In this phenomenon, the light behaves like a particle, transferring energy to electrons, which are ejected out of the material.
Summary on photoelectric effect
Physical phenomenon discovered by Heinrich Hertz in 1886;
Explained by Albert Einstein, in 1905, through the quantization of light proposed by Planck in 1900;
Electrons are ejected only if the energy of the incident photons is greater than or equal to the work function of the material;
The kinetic energy of the ejected electrons only depends on the frequency of the incident light;
Light intensity only affects how many electrons are ejected each second.
Do not stop now... There's more after the advertising ;)
History of the photoelectric effect
Around 1886, the German physicist Heinrichhertz (1857-1894) carried out several experiments in order to demonstrate the existence of
electromagnetic waves. To do so, Hertz produced discharges between two electrodes, and, on occasions, he realized that, when illuminated, the cathode was capable of producing more intense electrical discharges. Without knowing it, Hertz had discovered the photoelectric effect, through the emission of rayscathode.Two years after Hertz's observations, J.J.Thomson proved that the particles emitted by the illuminated plates were electrons. Therefore, thomson proved that the charge to mass (e/m) ratio of the cathode particles was equal to that of the electrons— particles discovered by himself a few years earlier.
Lookalso: The discovery of the electron
In 1903, Hertz's assistant, PhilippLenard, developed a series of experiments in order to establish a relationship between the light intensity and the electron energy issued, Lenard concluded that there was no dependence between the two things, which was to be expected, according to the knowledge of physics at that time. One year later, Schweilder he was able to prove that the kinetic energy of the electrons leaving the metallic plates was directly proportional to the frequency of light that illuminated them.
The results obtained experimentally contradicted the classical theory of electromagnetism and became a major challenge for physicists at the time for about 18 years. In the year of 1905, Einstein made use of a proposal presented by Planck, satisfactorily explaining the operation of photoelectric effect. The proposal used by Einstein is called quantization of the electromagnetic field. In the year 1900, Planck tried, in every way, to explain the black body issue, and was only able to do so by suggesting that light was quantized, that is, that it had energy values multiples of a smaller quantity. Although Planck understood that his feat was only a mathematical device capable of explaining a phenomenon physicist, Einstein believed that light really was formed by a large number of particles endowed with energy. In the future, such particles would come to be called photons.
After the publication of his article on the photoelectric effect, Einstein was awarded the Nobel Prize in Physics in 1921.
Know more about:What are photons?
Formulas
According to the corpuscular theory of light, proposed by Planck and used by Einstein to explain the effect photoelectric, light is made up of a large number of photons — massless particles that carry a small amount. power. This energy is proportional to the frequency of light and also to Planck's constant (h = 6.662.10-34 J.s), as shown in the following equation:
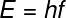
AND — photon energy
H — Planck's constant
f — light frequency
If the energy of a photon is large enough, it can rip electrons out of the material. The kinetic energy of an ejected electron can be calculated using the following equation:
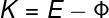
K — kinetic energy of electrons
AND — photon energy
Φ — job function
According to the above expression, the kinetic energy acquired by the electrons (K) depends on the energy of the incident photons (E) and also on Φ (occupationwork). This quantity measures the amount of potential energy by which the electrons are bound to the material, it is the minimum energy needed to pull them out. Therefore, all excess energy is transferred to the electrons in the form of energykinetics. Here it is important to realize that the kinetic energy acquired by electrons depends on exclusively gives incident light frequency and not the intensity of the light that is emitted.
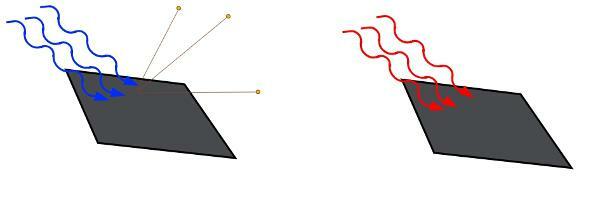
The frequency of light, not its intensity, determines whether electrons will be ejected.
work function table
Check out the measure of work function of some known materials. This function refers to the minimum quantity of energy required for electrons to be ripped from the surface of the material:
Material |
Job function (eV) |
Aluminum |
4,08 |
Copper |
4,7 |
Iron |
4,5 |
Platinum |
6,35 |
Silver |
4,73 |
Zinc |
4,3 |
Photoelectric effect experiment
Observe the figure below, it presents a simplified scheme of the experimental arrangement, used by Phillip Lenard, for the study of the photoelectric effect:
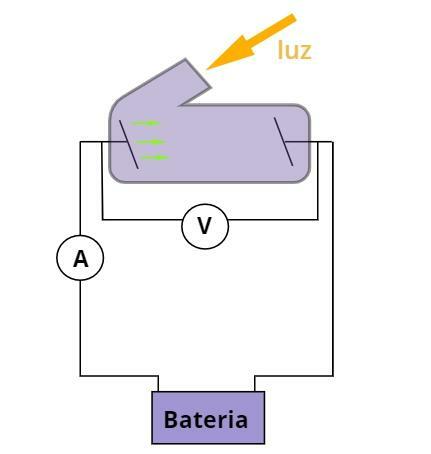
Experimental scheme used to study the photoelectric effect.
The experiment consisted of two parallel metal plates connected to a battery. In the circuit there were ammeters, used to measure the electrical current between the two plates, and voltmeters, used to measure the electrical voltage established by the battery.
When this battery was illuminated by certain frequencies of light, some electrons were emitted by one of the plates, which acquired positive charges (cathode). When accelerated by a potential difference provided by the battery, the electrons reached the other plate. This electrical current was measured by the ammeter.
Lenard noticed that with increasing light intensity, more electrons were ejected every second. However, keeping the frequency of light emitted by the light source constant, the energy with which the electrons were ejected did not change. Look at the chart below:

The saturation current corresponds to the number of electrons ejected by the illuminated plate each second.
The figure above relates to electric current produced by electrons, ejected by one plate and captured by the other plate, with the electric potential established between them. By applying this potential, the electrons that just left the plate, even with zero kinetic energy, reached the other plate. When all the ejected electrons reach the other plate, the electric current is saturated, that is, it starts to remain constant. What can be seen is that the saturation current depends on the light intensity: the greater the light intensity, the greater the electrical current formed between the plates.
However, when applying an opposite electrical potential, in order to delay the movement of the electrons that go from one plate to the other, it is observed that there is a minimum electrical potential (V0), called cutting potential, whereby no electron can reach the other plate. This indicates that the kinetic energy with which the electrons leave the plates does not depend on the light intensity. The maximum kinetic energy of the electrons can be calculated using the following equation:
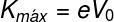
K — maximum kinetic energy of electrons
and — fundamental load (1.6.10-19 Ç)
V0 — cutting potential
Electron-Volt
Since the kinetic energy modules of electrons have modules too low to be measured in Joules, these energy measurements are routinely made in another much smaller unit, the electron-Volt (eV). The electron-Volt is the amount of electrical potential energy experienced by a charged particle with the lowest existing charge value, a fundamental charge, when placed in a region of electric potential equal to 1 V. Therefore, 1 eV is equivalent to 1.6.10-19 J.

In addition to the electron-Volt, it is common to use prefixes such as: keV (kiloelectrons-Volts, 103 eV), Me v (Megaelectron-Volts, 106 eV), TeV (teraelectron-Volts, 109 eV) etc.
Technological applications of the photoelectric effect
Several technological applications emerged based on the explanation of the photoelectric effect. The most famous of them is perhaps the photovoltaic cells. These cells are the basic units of the solar panels, through them it is possible to convert The light energy in electric current. Check out a list of the main inventions based on the photoelectric effect:
Photo-voltaic cells;
Relays;
motion sensors;
Photoresistors.
solved exercises
1) A substance, when illuminated by photons of 4 eV, is capable of ejecting electrons with energy of 6 eV. Determine the modulus of the work function of such a substance.
Resolution:
We will use the work function equation to calculate this quantity, note:
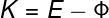
If the kinetic energy of the ejected electrons (K) is equal to 6 eV and the energy of the incident photons (E) equal to 4 eV, we will have:
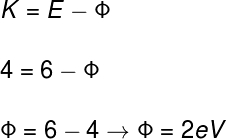
According to the calculation made, the work function of this material, that is, the minimum energy to eject the electrons, is 2 eV.
2) When we illuminate a metallic plate whose work function is 7 eV, we observe the ejection of electrons with energies of 4 eV. Determine:
a) the energy of the incident photons;
b) the frequency of the incident photons.
Resolution:
a) Let's determine the energy of the incident light photons through the work function:

B) To calculate the frequency of photons, we can use the following equation:

Taking the data provided by the exercise, we will have the following calculation:
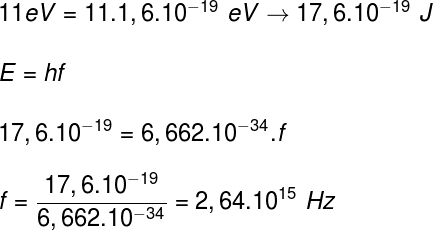
By Rafael Hellerbrock