You polygons are flat geometric figures formed by straight segments. You elements of a polygon are the mathematical objects that are part of its structure: points, straight and angles. convex polygons they have more elements than non-convex polygons, in addition to some unique properties.
Before we present the elements and properties, it is important to formally define the polygons. Come on?
definition of polygon
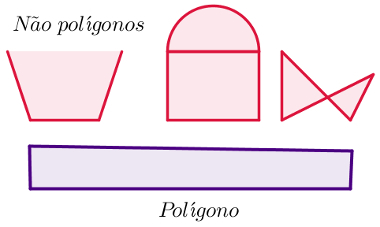
One polygon is a flat geometric figure that has the following characteristics:
It is made up of straight line segments only;
It is closed;
These line segments do not intersect.
In addition, a figure that has another meeting point between line segments, other than its extremes, can be seen as a set of polygons, but not as a polygon single.
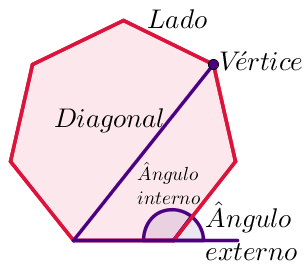
Elements of a Convex Polygon
all polygon convex has the following elements:
sides: are the straight segments that determine the polygon;
vertices: are the meeting points between two sides;
diagonals: line segments that connect two non-consecutive vertices of a polygon. Line segments that connect two consecutive vertices are the sides;
internal angles: are the angles formed inside the polygon, by two adjacent line segments;
outside angles: Are the angles formed on the outside of a polygon, by the extension of one side and the side adjacent to it;
Properties of convex polygons
The number of sides, vertices and angles (inside and outside) is the same.
THE sum of internal angles on one polygon n-sided convex can be obtained by the following expression:
S = (n – 2)·180
O number of diagonals on one polygon n-sided convex can be obtained by the following expression:
d = n (n - 3)
2
The sum of the measurements of the outside angles of a polygon any convex does not depend on its number of sides and is always equal to 360°.
By Luiz Paulo Moreira
Graduated in Mathematics
Source: Brazil School - https://brasilescola.uol.com.br/matematica/elementos-um-poligono.htm

