Well, we know that the elements that underlie analytic geometry are points and their coordinates, already that through these we can calculate distances, angular coefficients of lines and areas of figures flat.
Among the calculations of the areas of plane figures, there is an expression that determines the area of a triangular region using only the coordinates of the vertices of the triangle.
So, let's consider a triangle with vertices of any coordinates, and so let's see how to calculate the area of this triangle with just the coordinates of its vertices.

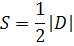
The parameter D is determined by the matrix of the coordinates of the vertices of triangle ABC.
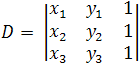
Note that the D parameter is the same determining matrix for checking the three-point alignment condition (see Three-point alignment condition).
Therefore, if you check the area of a supposed triangle and the determinant is zero, know that in fact these three points do not constitute a triangle, as they are aligned (that's why the area is zero).
An important observation regarding the expression for calculating the area is that Parameter D is in modulus, that is, we will use its absolute value. As it is an area, we should not adopt a negative determinant, as this will result in a negative area and that does not exist.
Let's look at an example for a better understanding:
“Determine the area of the triangular region whose vertices are points A (4.0), B (0.0) and C (2.2)”.

Therefore, the area of the triangular region of triangle ABC is 4 au (area units).
By Gabriel Alessandro de Oliveira
Graduated in Mathematics
Brazil School Team
Source: Brazil School - https://brasilescola.uol.com.br/matematica/Area-uma-regiao-triangular-atraves-determinante.htm
